NavList:
A Community Devoted to the Preservation and Practice of Celestial Navigation and Other Methods of Traditional Wayfinding
First sine table (Ptolemy)
From: George Huxtable
Date: 2009 Jan 21, 17:34 -0000
From: George Huxtable
Date: 2009 Jan 21, 17:34 -0000
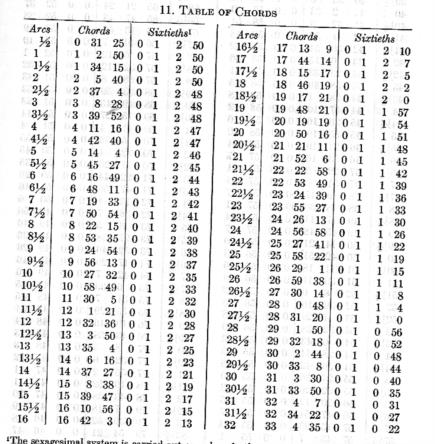
Hewitt Schlereth had asked about the construction of early mathematical tables, such as log tables. I wonder if the attached table will interest others, as it impressed me. It's a translation of part of a table from Ptolemy's "Almagest", which he wrote a few years after 150 AD Ptolemy didn't quite have our concept of sines, so it shows what he called a "table of chords", which, with an adjustment or two, is exactly the same as a table of sines of angles, to remarkably high accuracy. This table he used as a tool, in many places later in the Almagest, just as we would use sines of angles today. If a chord, across a circle of radius r, subtends at its centre an arc A, then the length of the chord is 2 r sin (A/2) (just sketch it to convince yourself). That's what Ptolemy has tabulated, for increments in A of 1/2-degree, over a range of 180 degrees, which is the maximum arc possible for a a chord. And he has taken r to be equal to 60 (arbitrary) units. To compare with a modern table of sines, then, we have to halve the arc A, shown in the left column. So that part of the table shown in the attachment, showing, in the left column, arc A in steps of 1/2 from 0 to 32, actually represents angles A/2 fom 0 to 16º in quarter-degrees. The rest of the table, in several further pages not shown, extends that angle A/2 to 90º, which is shown as a maximum in the left column of the table as an arc A of 180. What about the chords of those angles? Ptolemy had no way of dividing them into decimal parts, but he was familiar with sexadecimal divisions, which had been handed down from the Babylonians. So, after his units, in the left column of his chords, comes another column which is 60ths, and yet another column which is 3600ths of a unit. So to get to his exact chord-lengths, you have to take those fractions of the numbers given, and add them up. Finally, remember that these were chords of a circle of a circle of radius 60, diameter 120, so the maximum chord was 120 units. So to turn them into our familiar sines, we have to divide the given chord lengths by 120. It turns out that Ptolemy produced what we would now call a table of sines, to breathtakingly high precision. It's simplest to see by trying an example from the part-table in the attachment. Choose an arc at random, say 26 1/2 degrees, which corresponds to an actual angle of half that, 13 1/4 º. Now take Ptolemy/s chord, of 27 / 30 /14 units. Turn that into decimal units, as 27 + 30/60 + 14 /3600, or 27.503889 chord-units in decimal. Now divide by the diameter of 120 and we get 0.2291991. Compare that with sin 13.25º, for which a calculator gives 0.2292000. a difference just a bit over 1 part in a million! And that's not a fluke; if you make the same comparison for other arcs in the table, you will find corresponding precision, though I expect there may be a blunder ot two to be unearthed, if you examined every entry. The disbelieving should try a different angle, and check it out. I have attached only one-sixth of the complete table; if anyone would like the rest, just ask, or look at the website referred to below. I haven't mentioned the third column, which is nothing more than our familiar table of differences, for linear interpolation. He shows the difference in the chord that corresponds to a change of one 60th of a unit in each arc; that is, to a change in angle of 1/120 of a degree. These differences are shown, in the fourth column, down to one 216000th of a chord unit; a precision that's irrelevant, as I see it. How on Earth did Ptolemy do it? Remarkably, he used pure Euclidean geometry. From first principles, he derived the lengths of sides of regulat polygons inscribed within a circle. And then went on to show how chords of sums and differences of two angles could be derived from those, and built up his table in that way. He gives several pages of explanation, with diagrams. All this understanding soon became lost to Western culture when scientific knowledge succumbed to religious orthodoxy, and only survived in Arab / Persian cultures, through which it was returned to Europe over 1000 years later. My text comes from chapters 10 and 11 of book 1 of the Almagest, translated by Taliaferro, which comes with works of Coperrnicus and Kepler in "Great books of the Western World", 16, published by Encyclopaedia Brittanica, 1952 edition, pages 14-24. Fortunately, that translation of those very pages, with the full table, has been digitised and can be read at- www.cs.xu.edu/math/math147/02f/ptolemy/ptolemytext.html George. contact George Huxtable, at george@hux.me.uk or at +44 1865 820222 (from UK, 01865 820222) or at 1 Sandy Lane, Southmoor, Abingdon, Oxon OX13 5HX, UK. contact George Huxtable, at george@hux.me.uk or at +44 1865 820222 (from UK, 01865 820222) or at 1 Sandy Lane, Southmoor, Abingdon, Oxon OX13 5HX, UK. --~--~---------~--~----~------------~-------~--~----~ Navigation List archive: www.fer3.com/arc To post, email NavList@fer3.com To , email NavList-@fer3.com -~----------~----~----~----~------~----~------~--~---