NavList:
A Community Devoted to the Preservation and Practice of Celestial Navigation and Other Methods of Traditional Wayfinding
From: Robin Stuart
Date: 2019 Mar 8, 10:59 -0800
Andres,
Your reluctance to accept the suggestion that 1 LoP defines a Confidence Ellipse with an infinite axis
“Real world, not the imaginary one. Mathematics and the practicality of things”
might be understandable but it certainly does not apply to the case two LoP’s which in turn shows that your statement
“The ellipse of confidence, EoC, has math sense for three or more sights. Not for two.”
is simply not correct.
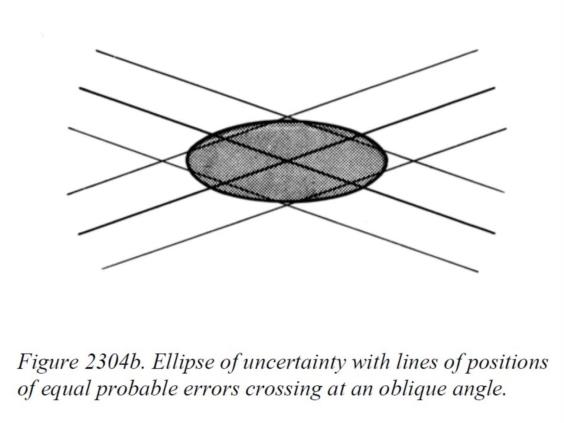
If this seems strange you might take a look at Chapter 23 of Bowditch 2002 entitled “Navigational Errors”. It contains Figure 2304b (p.343) copy of which is attached. It shows the ellipses of uncertainty or confidence ellipses constructed from 2 LoPs and should satisfy your requirements that things be discussed in a “nautical sense”. You will notice its similarity to the second of the figures I attached in my previous post and reattached here. Other standard references you may want to take a look at are
Daniels, H. E. (1951). The theory of position finding, Journal of the Royal Statistical Society, 13 B, 186-207.
Stansfield, R. G. (1947), Statistical theory of D.F. fixing, Journal of the Institution of Electrical Engineers-Part IIIA: Radiocommunication 94(15), 762-770.
Although Stansfield is talking about is radio direction finding he reduces the problem to one that is formally identical to the multi-LoP problem being discussed here.
I am intrigued by your formula sigma = K sqrt(1/(n-2)) and would like to know more about it. I am aware that the unbiased estimator for the population standard deviation from n samples is proportional to sqrt(1/(n-1)) but really don’t see how that is relevant here. Is there a reference that you could provide where this is justified and derived?
Robin Stuart
P.S. Actually our fixation on ellipses is a rather misguided. In all cases the observations define confidence contours that happen to be ellipses under certain approximations.