NavList:

Greg,

This PDF was just the sort of thing I was looking for, with a concise statement of the formulae for Bygrave.  That said, my first attempt at using the equations came up with nothing like what I got from Pub. 249.  I would appreciate you (or perhaps others) helping me sort out where I am making my errors.

First, I recast the equations slightly to make them fit the way my mind works.

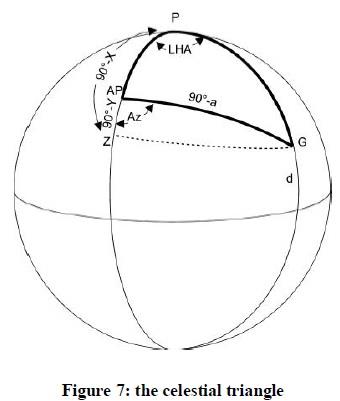
tan(x) = tan(d) ÷ cos(LHA)  I recast as

        1. tan(d) ÷ cos(t) = tan(x)

...where d = declination of the GP, and

            t = meridian angle

I inserted a line for myself of

         2.  lat ~ X = Y

...where I am looking for the difference between the latitude of the AP (i.e. "lat") and the latitude of point X.  This difference I designate as Y.

      3.  (tan(t) * cos(X)) ÷ cos(Y) = tan(Az);   

I inserted another line:

      4.  180 - Az = Z

...where Z is the azimuth angle to the GP (e.g. N 100° W).  From that, I can derive Zn, the azimuth (e.g. 260°)

Finally, where Ronald uses "a" in his final equation, I designate that as Hc.  Hence:

      5.  cos(Az) * tan(Y) = tan(Hc);   

I *think* I have wrapped my head around the equations...except that I come up with answers that don't match with Pub. 249.  So either I have misunderstood the equations, or I am not using my calculator properly.

Here is the scenario I used.

GP of the sun:   GHA = 48° 03.6'            Declination = N 11° 44.6'

AP = 53° N    114° 03.6' W

Hence, the meridian angle = t = 66°

1.  tan(11.743°) ÷ cos(66°) = tan(X)

      0.208 ÷ 0.407 = 0.511

      X = arctan(0.511) = 27.1°

2.  53° ~ 27.1° = Y

     Y = 25.9°

3. (tan(66°) * cos(27.1°)) ÷ cos(25.9°) = tan(Az);   

    (2.25 * 0.890) ÷ 0.899 = tan(Az)

    2.00 ÷ .899 = 2.22

    Az = arctan(2.22) = 65.8°

4.  180 - 65.8 = Z

      Z = N 114° E

5. cos(65.8°) * tan(25.9°) = tan(Hc);   

     0.410 * 0.485 = 0.199

    arctan(0.199) = 11.2°

Now, when I do this with Pub. 249, I get an azimuth angle "Z" of N 103° E and an Hc of 23° 44'.

Clearly, I am doing some things very wrong.  Do you observe what they might be?

Thank you for giving thought to this.

Bob

File: