NavList:
A Community Devoted to the Preservation and Practice of Celestial Navigation and Other Methods of Traditional Wayfinding
From: Robin Stuart
Date: 2021 Dec 29, 10:23 -0800
David,
Your thinking of the great circle equator crossing problem in terms of discs (or slices through the sphere) has merit but I don't see how it gives your stated result. If the latitude and longitude for the departure point are L1, λ1 and for the destination L2, λ2 then I get the longitude, λ, of the equator crossing point is
tan λ = ( sin λ2 tan L1 - sin λ1 tan L2 ) / ( cos λ2 tan L1 - cos λ1 tan L2 )
This equation has 2 diametrically opposite solutions and you need to select the one that applies.
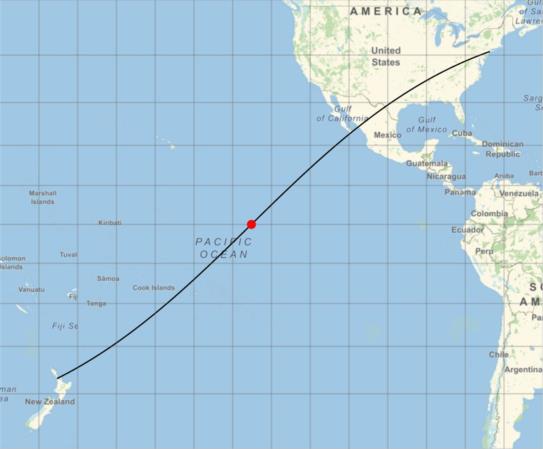
This was derived by working in 3D coordinates. A pole of the great circle can be found as the vector cross-product of the departure point and the destination. The longitude of the equator crossing point is the longitude of the pole ± 90°. To show that it works here's a plot of the great circle from Auckland to New York City; a route that Air New Zealand was planning to start around the time the pandemic hit. The red dot is at 135.2°W.
Regards,
Robin