NavList:

All,

 

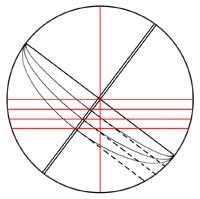
Samuel's recent questions about Aries and SHAs spurred me to brush up on my own understanding of sidereal time and that led to precession and nutation and somehow I ended up reading Bowditch (2002 ed.) chapter 19, § 1910: "Twilight". Toward the end of the second paragraph it reads, "More precise determination of the time at which the center of the Sun is any given number of degrees below the celestial horizon can be determined by a large-scale diagram on the plane of the celestial meridian, or by computation." I didn't even read the last part before I set the book aside and opened Photoshop to begin drawing a diagram (attached) for the current declination of the Sun and my latitude. I was almost done when I realized that all I was doing was determining the LHA from the declination, latitude and a given altitude...and I already knew how to do that on a calculator (or so I thought).

 

I used the formula for a time sight: LHA = cos^-1((sin(Ho)-sin(Lat.)·sin(Dec.))/(cos(Lat.)·cos(Dec.)) and the declination of the Sun at 15:00:00 UT1. So, on 19 Sep., 2014, cos^-1((sin(-6°)-sin(37°3.3')·sin(1°19.2'))/(cos(37°3.3')·cos(1°19.2'))) = 98°32.1'. Now, I reasoned that this must be the approximate LHA at evening civil twilight, so I divided the answer by 15 to get the number of hours past noon at the zone meridian then added 12 to that to get 18:34:08. I then added the time difference for my longitude (W076°28.6'-W075°), 1°28.6'/15 = 0:05:54 and the result was 18:40:03. Then, since I had already gotten the GHA of the Sun at 15:00:00 UT1 (76°34.1'), I subtracted 75° from that and divided by 15 to get the equation of time, +0:06:16, and subtracted that to get from apparent time to mean time, 18:33:47. And finally, I added 5 hours to get to the UT of local p.m. twilight, 23:33:47. Andrés' almanac app (which I trust) tells me p.m. civil twilight for my location will be 23:33:21. Pretty close. So, I tried subtracting the LHA in hours from 12 to get a.m. twilight. The result after the corrections for longitude and EoT: 10:25:30. Andrés' app gives 10:25:16. Also pretty close. I tried doing the same for a date of 21 Mar., 2015 and was equally as close to the app's predictions.

 

My question is, am I way off base here, or is this a reasonable way to approximate twilight times? Thanks in advance for any advice!

 

-Sean C.