NavList:
A Community Devoted to the Preservation and Practice of Celestial Navigation and Other Methods of Traditional Wayfinding
From: Robin Stuart
Date: 2016 Aug 8, 08:45 -0700
In an earlier post https://NavList.net/m2.aspx/Comments-BygraveMHR1-calculations-Stuart-aug-2016-g36126 I alluded to the problem of finding the LHA of a body’s rising or setting as not being doable on a cylindrical Bygrave or MHR1. It can however be tackled by a flat Bygrave.
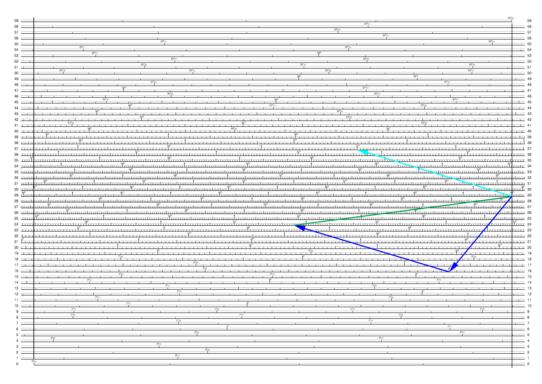
The required LHA satisfies the condition cos( LHA ) = -tan δ tan L. Take as an example δ = 75°S and L = 6°N which gives LHA = 66°54.3’. The attached diagrams show how this problem can be solved based of the scales in this post https://NavList.net/m2.aspx/Borrowed-Bygrave-Stuart-jan-2016-g34208 . Since log cot 45° = 0 the 45° point acts as the origin for the cotangent scale. Lines are drawn on the cotangent scale from 45° to 6° and 45° to 75°. These lines are then added vectorially (dark blue arrows) to produce the green line which is then transferred to the cosine scale by placing one end on either of the zero pointers A or B where it gives the required result.
I also attach a rough and ready spreadsheet I put together to aid in practicing with the model MHR1. Latitude, longitude, GHA and declination are entered in the “Control” tab and the values are passed to the “Bygrave”, “MHR1” (and “Modern”) tabs which compute altitude and azimuth according to the Bygrave and MHR1 instructions along with the necessary intermediate results. This is useful for debugging Bygrave/MHR1 calculations. Altitude and azimuth results are then written back to the “Control” tab in a common format for comparison. Bygrave and MHR1 calculations have been enhanced the method described at https://NavList.net/m2.aspx/Comments-BygraveMHR1-calculations-Stuart-aug-2016-g36126 to determine whether an object is above or below the horizon.
Robin Stuart