NavList:

Hello!

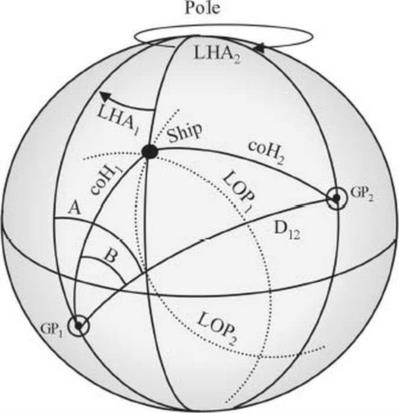
I tried the direct calculation of position - as per the "CELESTIAL NAVIGATION IN THE GPS AGE" by John H. Karl, Chapter 7, the Position without St.Hilaire article.

The formulas are:

cos(D₁₂) = sin(d₁) · sin(d₂) + cos(d₁) · cos(d₂) · cos(GHA₁−GHA₂)
(7.5a)

cos(A) = [ sin(d₂) − sin(d₁) · cos(D₁₂) ] / [ cos(d₁) · sin(D₁₂) ]
(7.5b)

cos(B) = [sin(H₂) − cos(D₁₂) · sin(H₁) ] / [ sin(D₁₂) · cos(H₁) ]
(7.5c)

sin(Lat_A±B) = sin(d₁) · sin(H₁) + cos(d₁) · cos(H₁) · cos(A ± B)
(7.5d)

cos(LHA₁) = [sin(H1) − sin(d1) · sin(Lat_A±B) ] / [ cos(d1) · cos(Lat_A±B) ]
(7.5e)

Lon = LHA₁ − GHA₁
(7.5f)

Where the GHA_i, d_i, H_i are the GHA, declination and H_Observed of the body_i respectively.

I guess - the H₁ and H₂ must correspond to the same moment in time. So in real life I will need either account for the MOB (the movement of body), for the MOA (movement of observer), or do both advancements to the H₁ before I may start using the formulas.

So I'm stuck here: I need to know the relative angle between my course T and the azimuth of body₁ to be able to obtain the correct value from the V[kn] · cos(Zn - T) · t[hour] formula. (The "V" is my speed, the "t" is the interval between the sights)

Is there a way to do it without any plotting at all? - here (the original "Death..." post) Frank still used some DR and paper graphs.

Thank you in advance.

Regards,

Tony

PS

All the formulas and images are by  John H. Karl.

File: