NavList:

Martin, a few days ago, you wrote:
"In the Dallas area, the total coverage took place around 18:44 UTC. After the eclipse, I calculated the GHA and declination of both the sun and moon with the following results:
GHA Sun: 100° 35.6’
GHA Moon:  100° 31.5’
Declination of the Sun: 7° 36.0’ N
Declination of the Moon: 8° 1.7’ N"

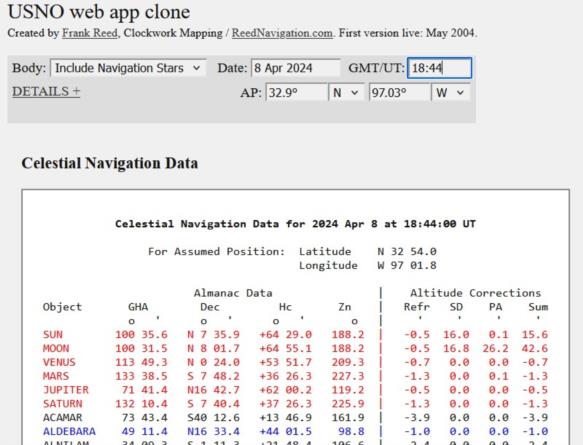
Looks good. And your numbers are a near perfect match for the data from my "USNO clone" web app (screen cap below; link here), so that's good. But they don't overlap?! Where's the eclipse?!

Ahh, of course, these positions differ by half a degree which tells us that if we had been in the Pacific west of Panama, south of Mexico (at the subSun point, longitude 100.6° and latitude 7.6°, looking at the Sun right at the zenith) we would not have seen an eclipse. To get the eclipse to "happen" at Dallas in the computed coordinates, we would need to look at some "apparent" coordinates, like apparent altitude and azimuth. They should match up.

Now the standard USNO data (cloned in my "clone") shows that the azimuths match, 188.2° for both Sun and Moon (see below), but it doesn't provide apparent altitudes. The true altitudes (Hc values) differ by 26.1'. The Moon is at a higher Hc. That doesn't seem too interesting at first, but then look at the altitude corrections. The difference between the Moon's parallax in altitude and the Sun's parallax in altitude is exactly the same: 26.1'. So sure enough, it all works. Thanks mostly to its parallax in altitude, despite the fact that their GHA/Dec coordinates differ by half a degree, the altitude and azimuth would line up perfectly, the Moon right on top of the Sun. And there's your total eclipse! :)

You added:
"and also because the moon moves in the sky at a rate 14.48°/hour instead of the sun that moves at a rate of 15°/hour, so the moon moves in the sky to the left relative to sun. "

Those numbers get you started, but once again they're geocentric, and the changing parallax of the Moon is a significant factor here. As it happens, since you were in Dallas, and the Moon and Sun were near due South at the time of the eclipse, it's less important than for other locations on the path of totality. Also, in general when thinking about the motion of the Moon relative to the Sun, planets, and stars (whether for eclipses or "lunars"), it's usually more useful to look at rates of change of SHA and Dec since SHA is "tied" to the celestial sphere.

Frank Reed

File: