NavList:

Martin Caminos, a few weeks ago, you wrote some thoughts about latitude and longitude. I had hoped someone else would answer, but that didn't happen.

You wrote:
"It would be interesting to me if anyone in the group knows when and why the latitude and longitude coordinate system was designed the way we know it."

It's old... really old. Some years after publishing his masterpiece on astronomy, known to us today as the Almagest, the Greek/Roman astronomer Ptolemy also published his Geography (this was probably around 150 AD). It listed the latitudes and longitudes of some eight thousand towns and geographic features in the known world extending from northern Europe through the core territory around the Mediterranean into Africa and as far as eastern Asia. It's worth noting that, as with the Almagest, we only have derivative copies of the Geography available today, all produced more than a thousand years after the original, based on copies of copies, so all the knowledge in the Geography has to be assumed to have some accumulated entropy (errors from the copying process) as well as some later improvements.

Ptolemy's Geography was a revision and expansion of an earlier geography by Marinus (and Ptolemy tells us so), but no copies of that work have survived. It is accepted, though, that this, too, was just one exemplar in a relatively long Classical Greek tradition of works compiling geographic knowledge. In many ways, Ptolemy's work was an apex document, a culmination of centuries of development, which helps explain why it lasted for over a thousand years as a reference work! The original concept of measuring terrestrial positions in a longitude-like and latitude-like coordinate grid almost certainly started with astronomical coordinates, probably in Babylonian celestial culture as early as 1000 BC or even centuries earlier. Certainly we owe the 60-based "sexagesimal" angular accounting system to them. Those coordinates were then presumably transferred to the Earth, the "globe", as the concept of the spherical Earth became accepted knowledge in Classical Greece. By the time of Eratosthenes (flourished c.225 BC, about 375 years before Ptolemy), who calculated the circumference of the Earth based on astronomical zenith distances and ground travel distances, the idea of the spherical Earth was certainly not new. He is often credited with the earliest "maps" based on latitude and longitude. As soon as the spherical earth/globe concept was normalized, the idea of measuring terrestrial latitudes directly from the astronomical "latitudes" of stars was obvious, and the problem of longitude was apparent, too.

Both Ptolemy and Hipparchus (three centuries before Ptolemy, c.150 BC) recognized that longitudes could be "scientifically" observed by watching the Moon. They weren't thinking of lunar distances yet, but the idea of observing lunar eclipses for longitude was described by both of them (see PS). It would have worked beautifully, but why bother? Until there was a means of live navigation in longitude, determining longitude on the spot, as required in a voyage, exact catalogues of longitudes didn't have much practical value. The longitudes (really longitude differences) in Ptolemy's Geography were all over-estimated by 50% or more. They were derived primarily by, what we would call, dead reckoning --travel times reported by traders and travelers in distant lands and along distant coastlines.

Martin, you also wrote:
"I would also prefer to measure latitudes (or declinations) from zero (at the north pole) to 180 at the south pole."

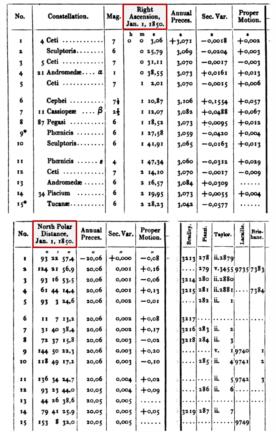
In some historical calculations, like for local time, it was quite common to have a small sub-calculation for "pd" or polar distance. That's on the right track, but it was only an auxiliary quantity in a calculation. However, there were occasional attempts to go further and do just as you say, running a polar angle that starts at zero at the north pole and runs to 180 at the south instead of our standard equatorial latitude or declination running to +90 at the north pole and -90 at the south. One major case in particular was the very popular "B.A.C." [British Association Catalogue] created, compiled, and almost completed (before his death) by Francis Baily in the years after he famously wrote about seeing "beads" during a total solar eclipse (yes, the Baily of "Baily's Beads"). The B.A.C. was one of the preeminent all-sky catalogues of relatively bright stars, basically the direct predecessor to the Yale Bright Star catalog. I'm attaching a sample of the first fiften stars in the B.A.C. and also the title page, highlighting the coordinates used.

The experiment with "north polar distance" ended with the B.A.C. or soon after. Although the catalogue was very popular, and, for example, some of its star numbers even appeared in "Norton's Star Atlas" first published in 1910, this eccentric feature of the B.A.C. did not last. The simple problem with "north polar distance" in place of declination was that it solved no "significant" problem. Significant? In terms of mid-19th century computations, it did solve a "real" problem. It made life easier by avoiding a sign in that coordinate. N.P.D. was always positive, or in the language of computations in that period when few people dealt with signs, it eliminated the "name" (N or S) on declinations. Every value in the column of "north polar distance" had the same name --all north!-- and thus no need for a name (or a sign). That's a benefit. But as it turned out the benefit was insignificant and confusing, even to astronomers. It didn't stick.

Modern navigators still worry too much about these coordinates, and modern navigation education practice still buries them in impenetrable jargon and astronomical terminology. Declination is the latitude of the subStar point. GHA is the longitude of the subStar point (with the caveat that GHA is always a west longitude).

Frank Reed

PS: Longitude by lunar eclipse: First of all, a key feature of lunar eclipses, different from solar eclipses, is that the events of lunar eclipses occur at the same absolute time (same UT) for all observers on one whole side of the Earth who have good weather. To get a longitude difference, we write to our friendly local astronomers and astronomy enthusiasts in distant lands and ask them to record the "local time" when the Moon enters or leaves the "umbra" --the deep shadow-- of the Earth. This can usually be timed to the nearest couple of minutes or by averaging entrance and exit, to the nearest minute (which, in modern terms, yields longitude to the nearest 0.25°). The local time is determined either as sidereal time, by observing what stars are on the local meridian at the time of the events (right ascension of meridian or zenith is identical to local sidereal time) or by using some basic physical clock (even a water clock or a sequence of sand-glasses can work) to determine the interval between the eclipse events and the nearer of sunset or sunrise. If I see the umbral eclipse begin at 21:15 local time, and you see it begin at 01:35 local time, then the difference in longitude between us is 4h20m or 65.0°. There are some small corrections, but that's the fundamental idea.

File:

File: