NavList:
A Community Devoted to the Preservation and Practice of Celestial Navigation and Other Methods of Traditional Wayfinding
Finding UT from a lunar eclipse
From: Roger W. Sinnott
Date: 2019 Jan 20, 21:48 +0000
From: Roger W. Sinnott
Date: 2019 Jan 20, 21:48 +0000
This topic was mentioned earlier by several people, and I have some practical suggestions that can be tried at tonight's lunar eclipse. Let's assume you are hopelessly lost and don't know your latitude, longitude, local time, or Universal Time (UT), and you have no nautical instruments either. But you do have a clock that runs. How can you find UT to better than a minute?
(1) Set the clock running.
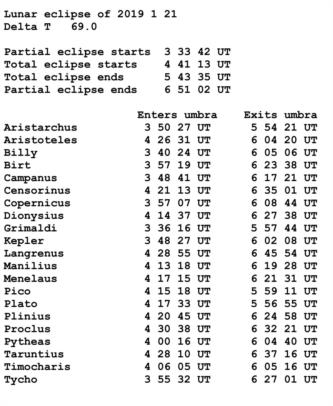
(2) Using the clock and your own observations, time to the nearest second some of the events listed in the table attached.
(3) Subtract each of your clock times from the predicted UT of that event in the table.
(4) Add up these differences and find the average.
(5) Applying this average to the clock's time, reset it to the UT you've found.
In step 1, the time shown on the clock is totally arbitrary -- you are determining the UT from scratch. But the arithmetic will be simpler if you set the clock to an initial estimate of UT, and even easier if you set it (say) to 10 minutes earlier than this.
In step 2, with the naked eye or binoculars, you'll only be able to time the first four events (that is, the umbral contacts with the lunar limb). But with a small tripod-mounted telescope you can make crater timings as well. The umbra's edge is not perfectly sharp. So the goal is to time when the middle of this "fuzzy" edge zone crosses the Moon's limb or the center of a crater or spot. The attached photo labels the craters for identification.
The four umbral contact times are from Helio Carvalho in Brazil, and the crater predictions are by me. All these predictions take into account the slight out-of-roundness of the umbra, which is literally the shadow of the oblate Earth. Also, they include a nominal 87 km added to the Earth's radius to allow for the silhouetting effect of the Earth's atmosphere. The figure of 87 km was arrived at by Dave Herald and me in an analysis of 26,685 crater and contact timings made at 94 eclipses between 1842 and 2011.
How close to the correct UT can you get by this type of observation tonight? I'd like to find out!
But note that the standard deviation of a single contact timing, historically, is about 1 minute with a telescope (and even more with the naked eye). The standard deviation of a crater timing is much better, about 25 seconds. This is why it is important to observe as many events as possible and take the average. It's also a very good idea to observe each crater at both entry and exit to cancel out certain types of errors.
I'm very interested in hearing from anyone who tries this experiment.
Roger
(1) Set the clock running.
(2) Using the clock and your own observations, time to the nearest second some of the events listed in the table attached.
(3) Subtract each of your clock times from the predicted UT of that event in the table.
(4) Add up these differences and find the average.
(5) Applying this average to the clock's time, reset it to the UT you've found.
In step 1, the time shown on the clock is totally arbitrary -- you are determining the UT from scratch. But the arithmetic will be simpler if you set the clock to an initial estimate of UT, and even easier if you set it (say) to 10 minutes earlier than this.
In step 2, with the naked eye or binoculars, you'll only be able to time the first four events (that is, the umbral contacts with the lunar limb). But with a small tripod-mounted telescope you can make crater timings as well. The umbra's edge is not perfectly sharp. So the goal is to time when the middle of this "fuzzy" edge zone crosses the Moon's limb or the center of a crater or spot. The attached photo labels the craters for identification.
The four umbral contact times are from Helio Carvalho in Brazil, and the crater predictions are by me. All these predictions take into account the slight out-of-roundness of the umbra, which is literally the shadow of the oblate Earth. Also, they include a nominal 87 km added to the Earth's radius to allow for the silhouetting effect of the Earth's atmosphere. The figure of 87 km was arrived at by Dave Herald and me in an analysis of 26,685 crater and contact timings made at 94 eclipses between 1842 and 2011.
How close to the correct UT can you get by this type of observation tonight? I'd like to find out!
But note that the standard deviation of a single contact timing, historically, is about 1 minute with a telescope (and even more with the naked eye). The standard deviation of a crater timing is much better, about 25 seconds. This is why it is important to observe as many events as possible and take the average. It's also a very good idea to observe each crater at both entry and exit to cancel out certain types of errors.
I'm very interested in hearing from anyone who tries this experiment.
Roger