NavList:

Lately I've been studying the possible error when using a 4-place haversine table, like the nice one Tony Oz has developed. In a typical calculation for celestial navigation, the last step gives you a haversine value and you want to know the corresponding angle.

Let's say your calculation gives a final haversine of 0.10390002..., which is extremely close to the 0.1039 listed in Tony’s table for 37° 36'. So you say, "What luck -- I don't have to interpolate! My answer is 37° 36.0' exactly."  But the real arc-haversine of 0.1039 (or 0.10390002) is 37° 36.5', a difference of 0.5'.

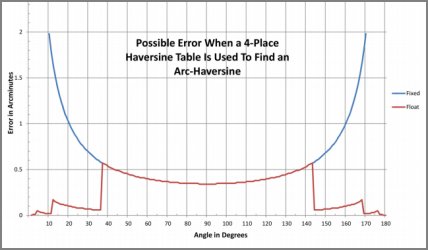
The attached graph shows the maximum possible error arising in this way throughout 0° to 180°. Conclusions:

  (1) The blue curve is for a fixed-point 4-place table, and we see that the possible error grows enormously toward 0° or 180°.

  (2) The orange curve is for a 4-place table like Tony's, where a barred symbol replaces any leading zeroes or nines. The improvement in overall accuracy is great.

COMMENT:  Between 37° and 143°, a simple way to improve the accuracy of Tony's 4-place floating-point table further is to add a 5th decimal place and omit the zero to the left of the decimal point. The columns would NOT get any wider. (This zero is often omitted in numerical tables anyway.)

Roger