NavList:
A Community Devoted to the Preservation and Practice of Celestial Navigation and Other Methods of Traditional Wayfinding
Re: Floating-Point 4-place Nat-Haversine Table
From: Roger W. Sinnott
Date: 2018 Dec 22, 16:46 +0000
From: Roger W. Sinnott
Date: 2018 Dec 22, 16:46 +0000
Frank,
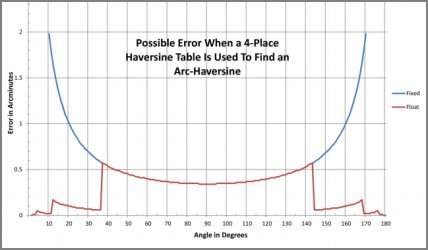
Exactly right! First I calculated M, the maximum possible rounding error in the haversines displayed in the table, using M=0.5*10^(-R-D), where D is the number of decimal places and R is the number of leading zeroes or nines omitted after the decimal point. Then, the maximum error in arcmin, E, is found from E=(2/sin(z))*M*3438, where z is the desired angle and 3438 is the conversion factor from radians to arcmin.
Just as you say, the 2/sin(z) term is the reciprocal of the derivative of the haversine function. It could be replaced by the reciprocal deriv. of any other trig function for which you want to make a similar error analysis.
I should have stressed more that the result is the maximum possible error in the vicinity of the angle z, and not the error at z exactly. In fact, the great majority of table lookups have a SMALLER error than E from this formula.
Exactly right! First I calculated M, the maximum possible rounding error in the haversines displayed in the table, using M=0.5*10^(-R-D), where D is the number of decimal places and R is the number of leading zeroes or nines omitted after the decimal point. Then, the maximum error in arcmin, E, is found from E=(2/sin(z))*M*3438, where z is the desired angle and 3438 is the conversion factor from radians to arcmin.
Just as you say, the 2/sin(z) term is the reciprocal of the derivative of the haversine function. It could be replaced by the reciprocal deriv. of any other trig function for which you want to make a similar error analysis.
I should have stressed more that the result is the maximum possible error in the vicinity of the angle z, and not the error at z exactly. In fact, the great majority of table lookups have a SMALLER error than E from this formula.
Roger
-----Frank wrote:-----
Nice graphic, Roger.
The shape of the graph should look familiar. That U-shaped curve is, of course, cosecant(x), which is another name for 1/sin(x). That makes perfect sense since the graph represents the change in the angle, x, for a given small change in the value of the "haversine(x)". The haversine is a simple variant of cos(x). Actually the haversine of any angle is (1-cos(x))/2, but its variability --everything that counts-- is directly proportional to cos(x).
Next do a tiny bit of calculus. The derivative of cos(x) is -sin(x), so then d(hav(x))/dx = sin(x)/2. And the inverse of that is 2/sin(x) --a curve proportional to cosecant(x), exactly as graphed, up to a constant of proportionality which is the result of asking for the result in minutes of arc for a change in the function at the fourth decimal place. and when you go from four-digit to five-digit, naturally the curve is reduced by a factor of ten, right?
Frank Reed
Original graphic, from Roger Sinnott's message: