NavList:
A Community Devoted to the Preservation and Practice of Celestial Navigation and Other Methods of Traditional Wayfinding
Re: Gnomonic Charts - Usable Zones
From: Stan K
Date: 2018 Jan 22, 10:50 -0500
From: Stan K
Date: 2018 Jan 22, 10:50 -0500
Just to quantify Frank's example, here are the Celestial Tools distance values:
Method 0 - 2390.5 nm
Method 1 - 2869.6 nm
Method 2 - 2588.8 nm
Obviously Method 2 is the better choice if Method 0 is out of the question.
But this is an extreme case. It is still not clear to me that Method 1 is always "nonsense". As it says in Celestial Tools Help, "Method 1 is easier to plot, but Method 2 results in a
But this is an extreme case. It is still not clear to me that Method 1 is always "nonsense". As it says in Celestial Tools Help, "Method 1 is easier to plot, but Method 2 results in a
shorter course. (In both methods, plotting is done on a gnomonic projection.)" OK, on a gnomonic projection, Method 2 is only marginally more difficult to plot than Method 1. 'Nuff said, I think.
Stan
-----Original Message-----
From: Frank Reed <NoReply_FrankReed@fer3.com>
To: slk1000 <slk1000@aol.com>
Sent: Mon, Jan 22, 2018 1:05 am
Subject: [NavList] Re: Gnomonic Charts - Usable Zones
Attached File:
Attached File:
Attached File:
From: Frank Reed <NoReply_FrankReed@fer3.com>
To: slk1000 <slk1000@aol.com>
Sent: Mon, Jan 22, 2018 1:05 am
Subject: [NavList] Re: Gnomonic Charts - Usable Zones
You wrote:
"FYI, both Method 1 and Method 2 of Celestial Tools are discussed in Bowditch, even Bowditch 2017, but only Method 2 is called "composite sailing"."
"FYI, both Method 1 and Method 2 of Celestial Tools are discussed in Bowditch, even Bowditch 2017, but only Method 2 is called "composite sailing"."
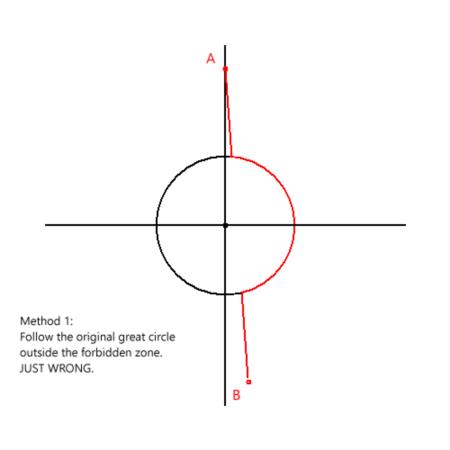
And to reiterate, a bit more bluntly, Method 1 is plain nonsense. It solves no meaningful problem. It's bad math. Of course, bad math is sometimes close enough for Bowditch. After all, if Bowditch tells us that 2+3=6, well, hey, we're not far from the truth! But it's pretty damn awful to apply nonsense ritualistically when the correct solution is available and easy to apply.
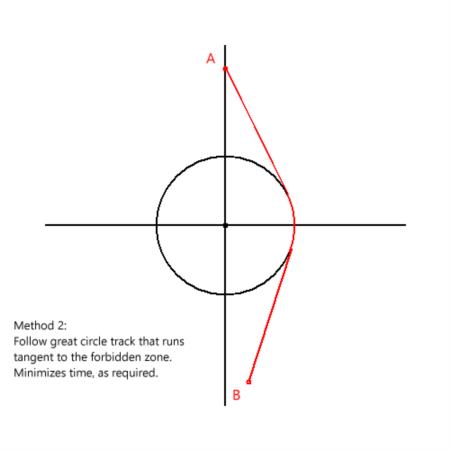
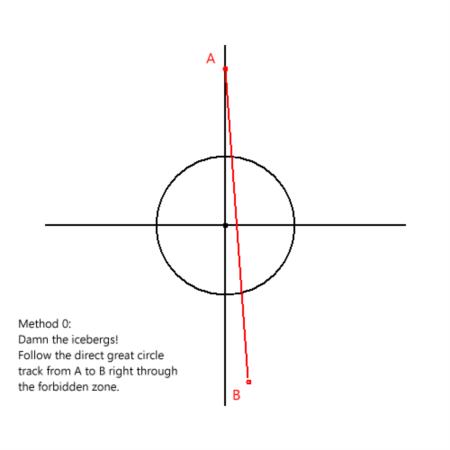
In the attached images, I have set up a case in high latitude where the difference is large and obvious. Point A is at 70°N on the prime meridian. Point B is at 70°N, 170°W. We want to take the most efficient path from A to B but --for whatever reason-- we are compelled to avoid latitudes above 80°N. In Method 0, we ignore the warnings and the compulsion and sail straight across. That's our baseline great circle path from A to B. In Method 1, we follow that same great circle path until we hit the limiting latitude of the forbidden area, and then we run around the edge until we pick up the the baseline great circle on the other side. This is nonsense even if it is in Bowditch. It's obviously the long way to travel. Finally in Method 2, we follow great circle paths on either side of the forbidden zone by selecting a great segment that is tangent to the forbidden zone on each side and running along the edge of the zone for the short arc in between. That's the correct mathematical solution to the navigational problem as given.
Frank Reed
Clockwork Mapping / ReedNavigation.com
Conanicut Island USA
Clockwork Mapping / ReedNavigation.com
Conanicut Island USA
Attached File:
Attached File:
Attached File:
