NavList:

Francis, you wrote:
"This is really a very interesting historical thing. Just found Dutton 1805 on Google who quotes the original Kelly method as described dating from 1797!"

What text did you find? Could I ask you to post the full title? I'm not aware of a "Dutton" from 1805. Of course, Kelly's graphical construction is well-known, but it had limited popularity. It seems to have been of greater interest to textbook authors than navigators.

You added:
"So you could do lunar clearance in 1797 easily using these simple graphical techniques?"

Not with Kelly's construction, no. It's almost the same issue as Breed's graphical system. The accuracy is abysmal, and it's not really easier than using tables. It's something that's intriguing, even "fun" for the right personality type, possibly pedagogically useful, but it doesn't solve any practical navigation problem.

And you wrote:
"Dutton claims they were accurate to 5’? Perhaps they were not? Otherwise why were they not taken up as routine? I shall look into it."

There may be some misunderstanding about what those 5' refer to. In good cases, this graphical method could clear a lunar with an accuracy of +/- 5' of arc in the cleared result, or at least that's the claim. That's not 5' in the position. An error of a tenth of minute of arc in clearing a lunar corresponds to approximately 12 seconds error in the resulting Greenwich time. An error of five minutes in clearing a lunar is fifty times greater or approximately 600 seconds in Greenwich time. At the equator, every four seconds amounts to 1 nautical mile error in longitude so this would yield an error in position of 150 miles or two and a half degrees of longitude. That stinks, and for what benefit? Tabular methods for clearing lunars were already well advanced by 1797, and they were no more difficult to work than Kelly's graphical method. And note that this mathematical error would have been on top of any observational error. I've seen suggestions that this graphical construction could serve as a test, proving or disproving work done by tables. But if you were a practical navigator, you could probably come up with a much better test: for example, having two people work the problem independently, or working the problem twice with different mathematical tables (something for which we have real historical evidence). 

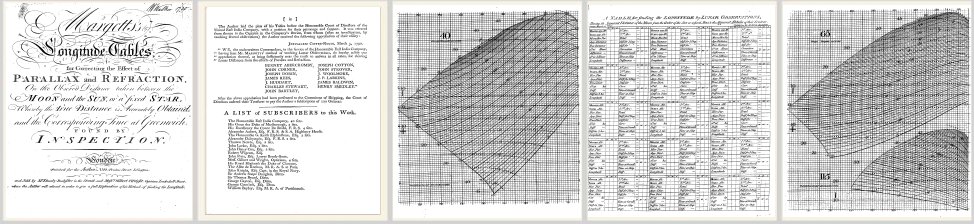
By the way, Ken Muldrew mentioned Margett's Tables which were originally published in 1790. These were not a graphical solution similar to Kelly's construction. Instead they were carefully engraved graphical tables. Such things were known as "linear tables" back then. I am attaching a copy (see below). One looked up the correction to a lunar in the graphical tables by finding the right curve on a chart. This is fundamentally not different from looking up the correction in a standard table by finding a number in the right row and column. Margett's tables are attractive, even beautiful, but they're not superior to ordinary lookup tables. The huge disadvantage of Margett's graphical tables was their cost. The lovely curves in his graphs all had to be engraved by hand by a team of professional engravers. It was an enormous project and all privately financed by Margett and his investors (subscribers). To recoop his expenses, the final product carried a price tag that put the tables out of the reach of all but the wealthiest navigators. It appears that they could not compete with the ordinary tables which were becoming widely available at this time. In addition, Margett's Tables were printed and sold in London which was also where marine time-keepers, soon to be known as chronometers, were mmost widely available. The competition from cheaper lunar methods from the low end and expensive machines from the high end apparently squeezed Margett's project out of practice and pushed Margett out of business.

A general comment:
It's been a while since we've discussed this, but I think it's worth remembering there's really a huge difference between the history of navigation and the history of published mathematical methods. Many odd little mathematical techniques have made it into print over the past few hundred years. But that alone is not evidence of practicality or actual use. If you want to know how navigation was actually done, then turn to the primary source materials. There are mountains of logbooks available for the past couple of hundred years, many now online, and they provide real, primary source evidence on the methods actually used in navigation. That said, there is a separate history of mathematical methods which can be fascinating and includes many arcane, minor, impractical techniques. Nothing wrong with that, so long as we don't confuse it with the history of navigation.

Frank Reed
ReedNavigation.com
Conanicut Island USA

File: