NavList:

Going back to Bruce Pennino's original post... Bruce, you wrote:
"I assume no onboard computer, GPS, etc."

Bring a four-inch globe. Stretch a thread from start to finish. You're done. In fact, you can get excellent results with an unmarked ball. Celestial navigation enthusiasts often jump for the most complicated solution, the one with the most tables and steps and trigonometry in it, the one that gives the "right answer". There can be only one!! A globe? Surely that's much too imprecise. Actually, it's just fine.

The historical cases we have of navigators obsessing over detailed great circle waypoints, like Lindbergh before his Atlantic crossing, are examples of ignorance, not excellence. Lindbergh didn't understand that he could get his great circle route from an ordinary globe. Furthermore, great circle paths offer advantages only in a few cases: distances of thousands of miles, locations in high latitudes, or locations that are nearly antipodal. As Gary pointed out, many great circle paths, like the last leg of Earhart's ill-fated flight, differ only insignificantly from a straight line drawn on any map. Even in middle latitudes, for example if you're sailing from Hawaii to Seattle, the difference between the great circle and the crude line on the chart is trivial, and weather planning would easily swamp the advantages supposedly offered by the great circle route. And yet one NavList member has told a story where he became the lone expert on a passage from Hawaii to Seattle who could select the course because he was the only one with the computational tools to generate great circle points. This is the triumph of computational obsession over navigational common sense.

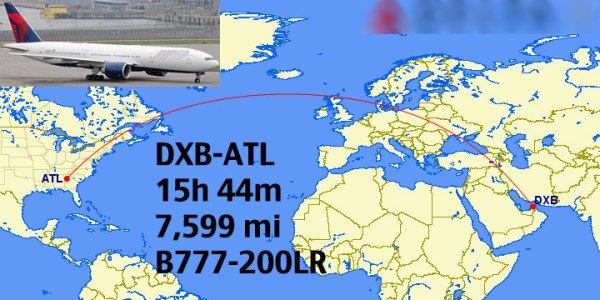
Naturally there are cases where a crude great circle path is unquestionably superior, like a flight from Dubai to Atlanta, which passes over the UK and not the central Sahara (which a straight line on a map might imply), but a common small globe is more than sufficient to make that determination and provide useful waypoints along the route. Navigators do not need perfect great circles. They need only rough approximations from which to select points that are efficient in terms of weather, logistics, and safety. 

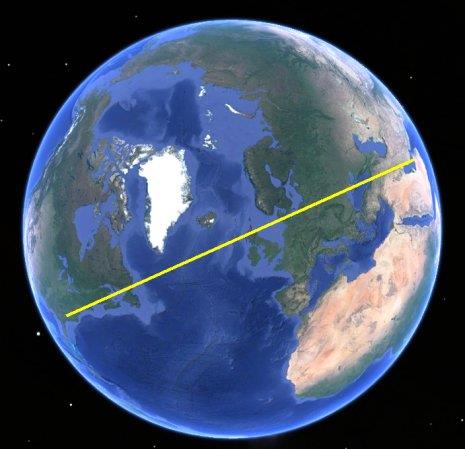
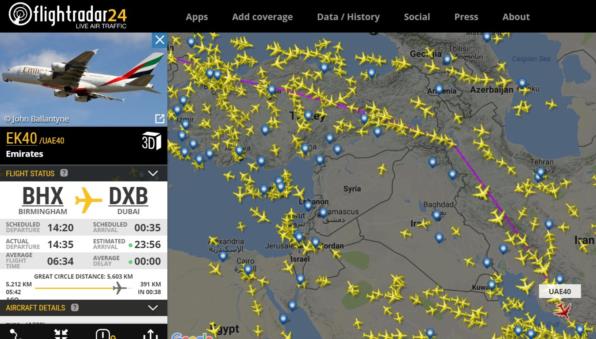
Suppose you have a globe but you don't have time to hunt for a thread to stretch across it. Or suppose you have quick access to a virtual globe, like Google Earth, but no other tools. You can find the great circle connecting two points by orienting the globe so that the start and destination points are placed on a straight line on opposite sides of the center of the globe as seen in projection or "from above". In the attached image, I've drawn an example approximating the great circle from Dubai to Atlanta. That's all there is to it. You can pick off as many waypoints as you need and choose them based on practical considerations in addition to their proximity to the great circle. Speaking of practical considerations, I'm also attaching a current image of approaches to Dubai showing a flight from the UK very carefully avoiding the great circle route since it passes over northern Iraq.

Frank Reed
ReedNavigation.com
Conanicut Island USA

File:

File:

File: