NavList:
A Community Devoted to the Preservation and Practice of Celestial Navigation and Other Methods of Traditional Wayfinding
From: David Pike
Date: 2016 Jan 20, 12:52 -0800
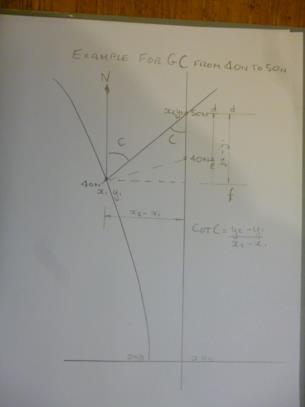
Robin. I think I see now what you mean. Am I correct in thinking that the points y1 &y2 apply purely to the construction of the nomogram and not the latitudes subsequently written on it? I.e. the distance y2-y1 is the distance df on my diagram attached not the distance de. Then we are talking about a right angled triangle after all, and everything fits. I was mistakenly thinking that the opposite side of the triangle had to be the line joining 40N to 40N in my diagram below. Forgive me for being dim. DaveP
David,
The diagram in question is a form of nomogram designed to evaluate or solve the second equation in the pdf file. It does not rely on or assume any particular projection. In a standard nomogram a line is drawn between 2 scales and the value where it intersects a third scale is the required result. In this nomogram the result is obtained by connecting points on the 2 scales and measuring the direction of the resulting line. Eq.(1.1) is simply the statement of that requirement.
"The fifth equation has x=0, so it must be the straight line up the centre."
Yes with values that increase like tan(L2) - exactly as seen on the chart.
"does that mean you’ve tried putting equations four and five into a function drawing programme to see what comes out?
That is indeed what it means,
Regards,
Robin