NavList:
A Community Devoted to the Preservation and Practice of Celestial Navigation and Other Methods of Traditional Wayfinding
From: Robin Stuart
Date: 2016 Jan 15, 07:50 -0800
David has it right when he points out that the gnomonic projection is not conformal (i.e. angle preserving) and so measuring directions against meridians does not give correct results unless one were to first transfer the great circle track onto a conformal projection, say mercator or stereographic, and measure the angles on that. If as an example we consider a great circle course from 32°N 65°W off Bermuda to 52° 0°E near London, measuring of the chart in question gives a bearing of 60°T whereas the correct great circle bearing is more like 46.5°T.
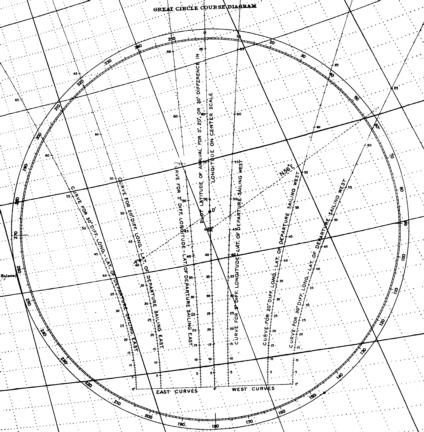
The image I attached to my previous post was the largest one I could easily find on the internet and only serves to show the form of the diagram for calculating courses. I have scanned the section of the chart in question and attach it here. I am still interested in understanding how and why it works. It might be a form of nomogram but would be unusual in that lines need to be shifted in parallel to read them. Verical distances along the central line seem to go like the tangent of the angle consistent with the gnomonic projection,
Robin Stuart