NavList:
A Community Devoted to the Preservation and Practice of Celestial Navigation and Other Methods of Traditional Wayfinding
From: Frank Reed
Date: 2022 May 6, 03:34 -0700
Antoine, you wrote:
"Here we are !
Computed Solution is close from :
UT = 11h22m at S00°27.9' / W092°44.8'"
Yes. Looks good to me! :) Notice where this is in the little chart below.
But it looks like you droppped a factor of ten in the uncertainty. You wrote:
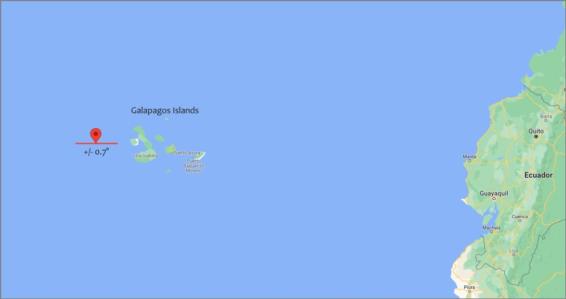
"Between 08h43 and 11h30 the geocentric observed Sextant distance changes from 1°24.4' to 1°30.8' , i.e 6.4' in 2.8 hours. If we consider that our sextant distance built-in error cannot be less than 0.1', this translates into an uncertainty of slightly under 30 minutes on the UT determination, i.e. an uncertaintly of 7° on Longitude."
That change of 6.4' in 2.8 hours is a rate of 2.3' per hour. If we can distinguish angles to the tenth of a minute of arc that means we can distinguish UT to 23 parts per hour or a bit less than 3 minutes of time. This implies a longitude uncertainty of about 0.7°. This also follows from noting that the Jupiter-Venus angular separation is changing at a rate that's about fifteen times slower than a lunar distance. With lunars, a tenth of a minute of arc corresponds to 12 seconds of UT or 3 minutes of arc in longitude (under best possible circumstances). If we slow that rate down by a factor of 15, then the expected uncertainty in longitude would be 15 times worse or again about 0.7°. I added error bars for that (minimum) longitude uncertainty to the chart below.
Frank Reed
Clockwork Mapping / ReedNavigation.com
Conanicut Island USA
PS: For anyone following along, a reminder: my Lunars workshop is running online this week (Atlantic session tomorrow and Sunday; Pacific session Mon,Tue,Wed).