NavList:

Nice puzzle, thanks!

Not sure how we could determine the time precisely but assuming the base of the church to be at about 2° elevation, coincident with the lower limb of the Moon, the (apparent) centre of the Moon would be somewhere around 2¼°, which makes the time about 16:47 UT. However, the elevation estimate is crucial in the time estimation, so we'll check it at the end.

At 16:47, the azimuth of the Moon, as seen from the church, is about 57.5°. Its (horizontal) diameter, which should be mostly unaffected by refraction, is about 271px (~ 30'), which makes the scale about 9.03 px/arcminute.

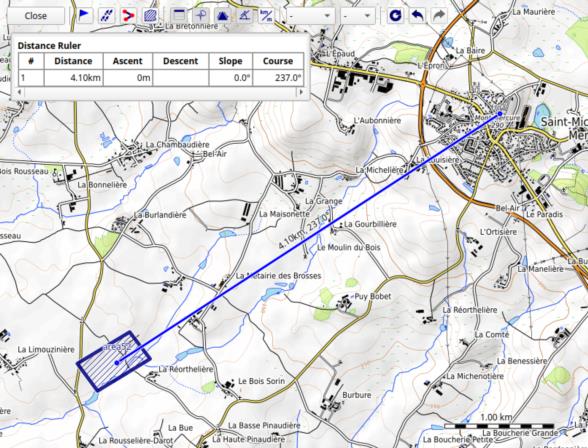
The steeple appears to be about 394px tall, and that angular size corresponds to the distance of about 4.10 km. It's also about half a degree to the left of the centre of the Moon, so the bearing to the photographer will be about 237°.

Given the uncertainty in time, the uncertainty in the azimuth of the Moon will be about a degree or two. The uncertainty in the distance comes from the unclear location of the bottom of the church in the picture; let's make the error about ±10%.

The resulting error box is in the attached picture, centred around 46°48.7' N and 0°55.7' W. It's smaller than I expected.

Now we can circle back to the original assumption of the elevation. The altitude of most places in the error box is around 126 m while the altitude of the hill is 290 m. At 4.1 km, this comes out to about 2.29°, which means that the Moon will be a bit higher than I assumed, and a bit more to the southeast, which means that the true location should be closer towards the NW corner of the error box or a bit beyond it.

Perhaps the picture was taken from that road?

File: