NavList:

David Pike, you wrote:
"Alternatively, is it a perfectly normal photo of a crescent Moon, whereas many photos utilising the Moon in the background have it artificially enhanced?"

Yes, it is a perfectly normal photo of the Moon. Remember half a degree is quite a small angle. Try this: hold something half a centimeter in diameter at a distance half a meter from your eye from the comfort of your living room without the actual Moon to compare against. Note how tiny that is! That angular size is 1/100 as a pure number (often called or 0.01 "radians") which you can convert to minutes of arc by multiplying by 3438, as always. The result is 34' which is about 10% larger than the average angular size of the Moon. We almost always over-estimate how big the Moon should look.

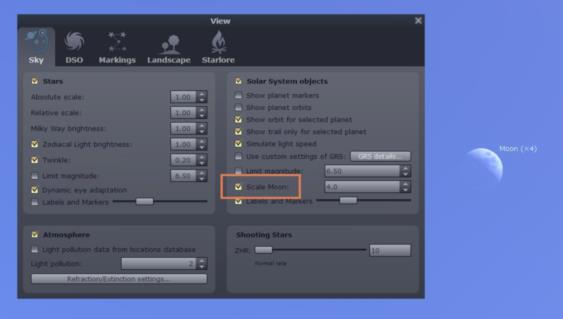
Many photos artificially increase the size of the Moon in post-processing. Other photos are taken using telephoto flattening of distance which creates an illusion of a larger moon without messing with the pixels. Why do these things? Apparently, to satisfy the viewer's expectations, which have been formed by the classic "moon illusion". Similarly in planetarium projections, the Moon is almost always displayed two to four times larger than its actual angular size. When I do planetarium presentations, I frequently use this as an opportunity to talk about the tides since the tidal acceleration from any astronomical body is proportional to the object's mean density and the object's angular diameter cubed *. If the Moon were three times larger in the sky than it actually is, the daily tidal range would be approximately 27 times larger than it is now. The desktop "planetarium app" Stellarium also includes the option to magnify the Moon for visual impact as seen in the image below.

Frank Reed

* the usual expression for tidal acceleration per unit distance is GM/r³, where M is the mass of the body (Sun, Moon, planet, etc.) and r is the distance to it, but if you replace M by density·volume you get an expression proportional to ρ·(R/r)³ where ρ (rho) is density and R is the object's linear radius. That expression is then proportional to ρ·α³ where α (alpha) is now angular diameter. The classic example of this is the comparison of the tides from the Sun and Moon. Since those object's have nearly identical angular diameters, their relative tidal accelerations are proportional to the mean densities of the Sun and Moon. Thus by observing that the Sun's tides are weaker than the Moon's by more than a factor two, it was understood at an early date that the Suns mean density was less than half the mean density of the Moon.

File: