NavList:
A Community Devoted to the Preservation and Practice of Celestial Navigation and Other Methods of Traditional Wayfinding
From: UNK
Date: 2014 Jun 6, 08:33 -0700
Another try at no-table navigation - that's not very precise.
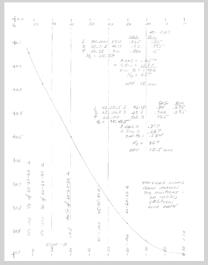
I tried starting with some known angles and sketched a curve of sine’s and cosines to do sight reductions with no tables.
Sine 90 = 1
Sine 0 - - approaches zero but doesn’t get there.
Sine 45, from a 45-45-90 triangle, is 1/1.414 = 0.707
Sine 22.5, from the half of the triangle above, is 0.382
Sine 30, from a 60-60-60 triangle split in half is 0.5
Sine 60, from the triangle above, is 0.866
We can split right triangles, leaving the 90 Deg angle, forever and get
Sine 15 is 0.277
Sine 7.5 is 0.143
These are all the angles I could get from memory right now.
I sketched out a fair looking curve of Sine’s <’s also equal to Cos (90-<). I used an adjustable curve to draw the line. At this point I put in a few more points to help with the curve.
See attachment of a no-table sine and cosine curve. The original is on a quad-ruled sheet and is easier to use than this scan.
I worked two examples on the attachment using the curve to get the sine and cosine values and to look up Hc. I used a calculator to do the multiplication. This attached curve is better than what you could do on a boat but I was still off 58 NM and 18.5 NM on the two examples. On a truly hand-drawn curve, you might do well to get within 1 to 2 degrees. This is better than nothing. At least you’d know when you were getting close to shore.
Hanno’s table is much better. It has accurate steps of every 0.573 degrees.
Regards, Noell