NavList:

Paul Hirose,

I will say that this is a quagmire for lunars. As I've written previously, you have to do some modeling that would be "tricky" and involve quite a lot of supposition and guesswork on top of some detailed limb analysis. The lunar limb is the limit of lunars, not something that we can really hope to fix. But you've hit on something in your latest comparison trials. Have you noticed that the Occult software is just awful?? With the tools you have created, you could build a much better lunar occultation analysis tool. 

Back to lunars and the lunar limb for a few minutes...

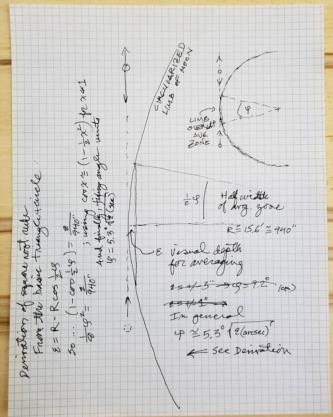
I opened a folder (an actual paper folder) on my desk today that said "lunar limb" and two pages in was a drawing I made (months ago? or years ago?!) that was just what I was looking for. I'm attaching a photo of it here. It's just some geometry to calculate the width of the "contact sector" for a lunar given some assumed minimum overlap depth. The idea is that if I bring a star or the limb or the Sun or the center of a planet's disk to the Moon in a lunar and sweep it back and forth, scraping it along the lunar limb to decide best contact, I'm really trying to get an almost imperceptible overlap with the Moon's limb. That's how we "sample" the actual limb of the Moon with its plateaus and valleys and other undulations. And the width of that contact zone can be described as an angular width --a sector width-- at the center of the Moon's disk. 

The math matches your chosen estimate rather well. You suggested that you "guessed 8°, that is, 4° either side of the true tangent point". If I select an overlap of +/- 3 seconds of arc, which is reasonable for high-quality lunars, then the overlap sector width would be about 9.2°. For small angles (anything under 10°), the sector width scales in proportion to the square root of the chosen overlap depth. So if we go with +/-1 arcsecond instead of +/- 3, then the sector width is reduced by a factor of about 1.73 (square root 3). That implies a sector width of 5.3°. 

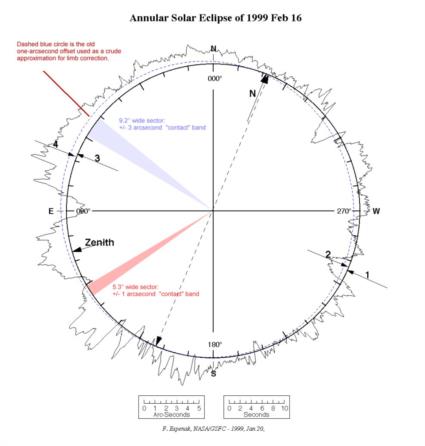
Next I took the Espenak eclipse diagram with its limb profile from that eclipse in 1999 which I posted a couple of days ago. I sketched in those two sector widths at random locations. Now just imagine sweeping them around to various different orientations on the lunar limb. You can see that the "average" limb sampled over the sector width would differ the mean limb by anywhere from about +3" to -2" for this particular eclipse, as it would also for arbitrary directions for lunars. Other eclipses show different profiles depending on the exact orientation of the Moon's face (the lunar "libration" angles). Similarly for lunars, you would have different limb profiles depending on the "libration".

So what should you use: one arcsecond of overlap? Three arcseconds? More? Less? There's no real answer. But one thing we can say with some certainty: higher magnification and greater observation quality has an interesting counter-productive side at this level of lunars. If you magnify more, you can make a more perfect contact with the Moon's limb, but you end up sampling a smaller arc along that limb with greater variability in the limb profile. There's no "pure" astrometric approach here. The Moon is lumpy. And when we magnify it, the lumps are more obvious.

Frank Reed

Note: the "displaced circular limb" was included in Espenak's old diagrams. It's a dashed circle shifted about one arcsecond. You described it as follows: "The Moon position from Lunar is the position of its center of gravity. However, that point is a little different from the mean limb center of figure. " Bear in mind that this old offset was just a "hack" (in the sense of a cheap solution). It represents a rough-and-ready average limb correction useful for eclipse predictions from the era when high-quality limb profiles were not available (before the Kayuga and LRO altimetry missions). The hack still has some merit, but only if used with the understanding that it it's an approximate limb profile.

File:

File: