NavList:

I have not yet read the numerous replies to this problem posted here.

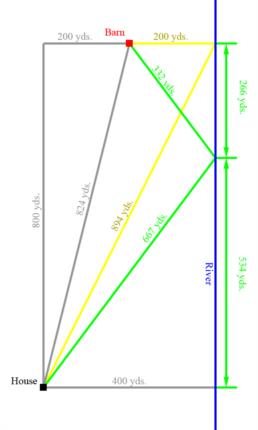
So, here is my solution so far - and my reasoning for it (reference the attached diagram):

At first, I thought perhaps it would be reasonable to travel straight to a point on the river which is parallel to the barn and then travel straight to the barn. The distance of the first leg could be found using trigonometry - which I believe the farmer would have access to.

We first need to find the angle of the course from the house to the point on the river which is parallel to the barn. So, we divide the north-south distance by the distance from the house to the river: 800 / 400 = 2. Then, we find the arctangent of the result: atan(2) = 63.43494882°. Next, we find the length of the course by dividing the north-south distance by the sine of the angle: 800 / sin(63.43494882) = ~894 yds. [the yellow diagonal]. Add to this the 200 yards required to travel from the river to the barn and we arrive at about 1,094 yds.

Then I thought perhaps it would be quicker to travel straight to the barn, then to the river and back to the barn. So, we divide the north-south distance to the barn by the east-west distance to the barn: 800 / 200 = 4. Then, we find the arctangent of the result: atan(4) = 75.96375653°. Again, we find the length of the course by dividing the north-south distance by the sine of the angle: 800 / sin(75.96375653) = ~824 yds. [the grey diagonal]. Add to that the trips to and from the river (200 yds. + 200 yds. = 400 yds.) and we arrive at a distance of about 1224 yards. Although the trip straight to the barn was shorter, the added distance of traveling to and from the river makes the total distance about 130 yards longer.

Then it occurred to me that it might be more efficient to travel directly to the mid-point on the river between the house and the barn (400 yards north of the house) and then straight to the barn. Or ... maybe there was some other point along the river which would result in a shorter trip. I could try some trial and error calculations which would lead me to the answer. Or, I could make a spreadsheet with a slider for the point on the river which would instantly allow me to see the varying distance. I chose the latter.

After a few seconds moving the slider back and forth, I discovered that a point on the river 534 yards north of the house (and 266 yards south of the barn) would result in a trip distance of 1,000 yards [the green diagonals]. This, of course, is less than either of the two methods I had tried before. And - as of right now - I can think of no other shorter route. For a moment, I entertained the idea of a circular route - but then I thought "No. That would be nonsense."

As for how a medieval farmer would arrive at this solution (without, of course, access to a computerized spreadsheet) - I have a vague idea involving a bit of string and a nail.

Now ... I will read the rest of the responses by much more learned men than myself, and I am sure I will be humbled (and probably a bit embarrassed).

-Sean C.

File: