NavList:

Pär Leijonhufvud, you wrote:
"I've thought of doing the math for calculating the error (it is, after all, just three bodies :-) ), but decided that I'm just too rusty to do the math. So I have actually started doing about the same thing you are: keeping a record and seeing where I end up. Of course, I only get data for 63N,  whch may or may not affect the dependability of the results. I have used it sucessfully above the arctic circle, but did not have the chance to determina actual error (in the woods and comparing to pole star 68 degrees above horizon with no tools...)"

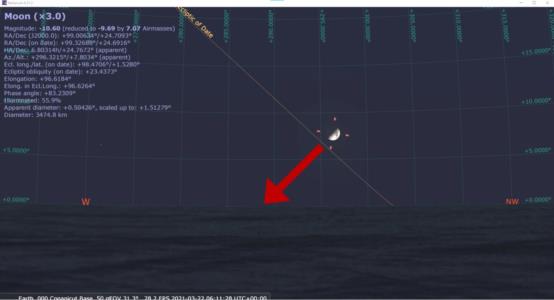
It's the 21st century. We can simulate all of this with ease in various desktop "planetarium" apps, including, for example, Stellarium. In the attached image, I have simulated a special case of the Moon's position as seen from my location here on Narragansett Bay (Rhode Island, USA), which is a nice "mid-latitude" test case (41.5°N). The special case I selected has the Moon near half-illuminated so that it's quite easy to visualize a line through the horns. I have also picked a date when the Moon is near the Gemini-Taurus border which guarantees relatively high declination. As you can see in the image, the line through the Moon's horns hits the horizon near an azimuth of WNW, something like 19° north of west and nowhere near South, where an observer with this basic rule in hand might expect. This would count as a disastrously poor compass. 

The problem here is not the Moon. A line through its horns points regularly and reliably to points quite close to the north and south ecliptic poles. While those poles are 23.5° from the proper celestial poles, which are always due north or due south, the ecliptic poles are close enough for general direction finding, and also, for the expert, the method can be expanded to get closer to true north with a few simple additions.

The problem here is the idea of tracing a line down to the horizon and then stopping there. It just does not work! Don't do it. Don't do it with the horns of the Moon. Don't do it with the Orion North Arrow. It fails dramatically for the horns of the Moon, as you can see in the image below, and it fails somewhat less, but still significantly, for the Orion North Arrow. The way to fix all this is to teach it properly and convince the folks peddling survival advice to get it right, too (this is probably hopeless, but if you explain that they're putting lives at risk, maybe...). 

So how do we get it right? Pull a pen or pencil out of your pocket or grab any straight stick off the ground (or your thumb can work, too, if you can hold it up at 90° to your forearm). Hold that stick in your fist "sideways" with your arm out-stretched. Aim your arm at the Moon, holding the stick in your firt so that it is approximately perpendicular to your out-stretched arm. Now rotate your hand until the stick is aligned along the line through the horns of the Moon. That stick is now aligned with the axis of the ecliptic. It is aligned perpendicular to the plane of the Solar System, which is a crude, but useful, approximation to north/south.

So now what?! Your north-south pointer is way out there at the end of your arm in your clenched fist. What good is that? There are a couple of options here. One, ask a friend to sight along it. That stick is pointing north-south (-ish) but it's also tilted "up" at some angle (like a three-dimensionally "free" magnetic compass needle that senses both magnetic direction and magnetic dip, too). Sight along it for direction, and you've got a good estimate for north-south. If you're alone, just "retract" your arm, being careful to maintain the stick "parallel to itself" in three dimensions. This is really quite easy: just pull your arm in without changing the axis of the stick. Draw it in close, then see where it's pointing. There are two components to this "pointing" direction: one part is "left-right" while the other is "up-down". The "left-right" portion is showing you north and south, with that caveat that it's really indicating the directions of the ecliptic poles.

All of this also applies to the Orion North Arrow, but it works better. These methods give you a three-dimensional pointer in space, aligned more or less (less with the Moon!) with the rotational axis of the Earth. And incidentally, the "gnomon" or shadow stick of a common sundial has the same three-dimensional alignment. It's tilted at an "up angle" towards the celestial pole while its "left-right" alignment shows true north-south.

Frank Reed

PS: Ecliptic poles? What are those? They're the points 90° away from the ecliptic. If you look at the Solar System with the orbit of the Earth as a flat plane and all the other major planets more or less in the same plane, the ecliptic poles are straight up and straight down from that plane. In terms of visualizing them on the sky, the ecliptic poles are 23.5° away from the familiar celestial poles (which are directly above the north and south poles on the Earth's surface). The north ecliptic pole is in the constellation Draco just about two-thirds of the way from Polaris to Vega. The south ecliptic pole is close to the Large Magellanic Cloud and lies about two-thirds of the way from the very faint "South Pole Star" sigma Octantis (now known officially by the IAU as Polaris Australis) towards Canopus. And although the Moon does not orbit exactly on the ecliptic, its horns point to those spots among the stars -- the ecliptic poles.

• North Ecliptic Pole: two-thirds of the way from Polaris toward Vega and 90° from the point on the ecliptic near the Sagittarius/Scorpius border,
• South Ecliptic Pole: two-thirds of the way from "Polaris Australis" toward Canopus and 90° from the ecliptic at Gemini/Taurus border.

File: