NavList:
A Community Devoted to the Preservation and Practice of Celestial Navigation and Other Methods of Traditional Wayfinding
From: Bill Lionheart
Date: 2020 May 16, 17:59 +0100
Bill,
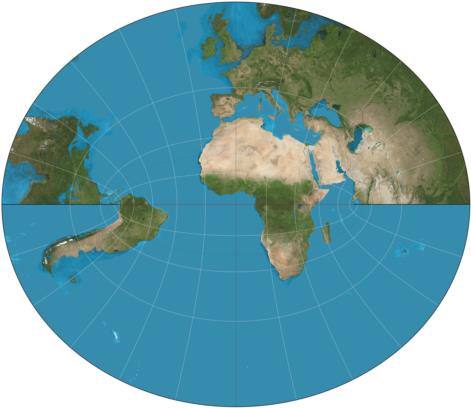
Thanks for providing these entry points into the Littrow projection in your post. This was new to me. As pointed out in the reference you provided it has some interesting properties. "If the complex z-plane is the Littrow map and the w-plane is the polar stereographic map, then z = w +1/w". This means that on the Littrow map both the north and south poles are pushed to infinity. In passing note that the Mercator projection is ln(w). Because both the Littrow and Mercator projections are analytic functions of the stereographic projection they must be conformal or angle preserving.
The article also mentions that the Littrow map is a "two-sheeted Riemann surface" which explains why land forms are cut off in the projection attached below. You presumably have to make 2 circuits of the equator before you get back to where you started from.
Of more direct relevance to navigation, the grid lines of the Littrow map form Weir's Azimuth Diagram described here.
Regards,
Robin