NavList:
A Community Devoted to the Preservation and Practice of Celestial Navigation and Other Methods of Traditional Wayfinding
From: Brad Morris
Date: 2017 Feb 3, 16:08 -0500
Brad,
It appears that the pdf is freely available at the link given by Andres. The underlying idea is amazing only in its bone-headedness and you’d wonder why people ever attempted to advance LoP’s on the sphere in the first place and how they got it so wrong in the process.
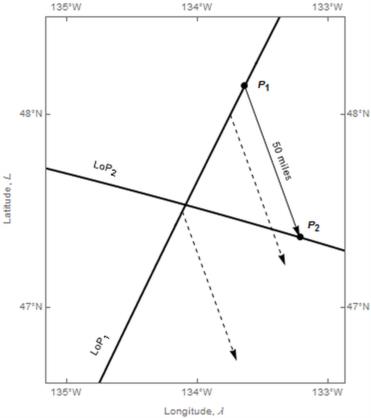
The procedure given in the paper is numerical but can be described in graphical terms. Draw the two LoP’s just as you obtain them. Then find a point P1 on the first LoP and P2 on the second separated by the known course and distance of the run. No need to advance anything. This is shown in the attached file.
It ultimately boils down to numerically finding the root of a non-linear equation in just one variable and is easy to achieve by standard iterative methods. The dotted arrows in the diagram are starting values used to initialize the iterative procedure. What might be a bit surprising is that, thanks in part to some fairly recent developments for calculating ellipsoidal arc lengths, it is feasible in practice to push this forward for the ellipsoid and it’s only modestly more complicated than the case of a sphere.
Regards,
Robin Stuart
Attached File: