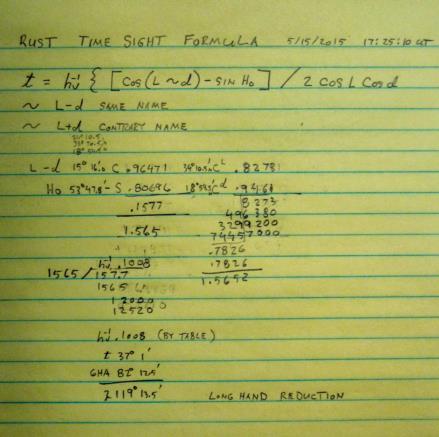NavList:
A Community Devoted to the Preservation and Practice of Celestial Navigation and Other Methods of Traditional Wayfinding
From: Greg Rudzinski
Date: 2015 May 15, 15:58 -0700
Francis,
See this example of the Rust time sight formula done longhand with a single 4 place multiplication and a single 4 place long division. Should be easy to do with the Ottis King slide rule.
Greg Rudzinski
From: Greg Rudzinski
Date: 2015 May 15, 12:12 -0700Francis,
The most elegant time sight formula to try and modify to all haversines would be the formula used in Rust's 1918 Practical Tables for Navigators and Aviators.
hav t = (Cos (Lat. ~ Dec.) - Sin Ho) / 2 Cos Lat. Cos Dec.
~ same name (Lat. - Dec.) ~ contrary name (Lat. + Dec.)
If Lars is watching then maybe he can work up something that will look good.
Greg Rudzinski
From: Francis Upchurch
Date: 2015 May 15, 07:59 -0700Question for I think Hanno +/-Greg.
Could the Doniol method be adapted for the Time sight reduction? I've been playing around with Fuller slide rule using the cosine formula
cos(LHA)=[sin(alt) - sin(dec)·sin(lat)]/[cos(dec)·cos(lat)].
Works fine but takes longer than LOP (Hc) using Bygrave or Brown-Nassau.
I like the old 19th century methods using trig logs and haversines, the formula I have is hav.LAT=logsec.lat+logcsc.p+logcos.s+logsin(s-alt). where p=polar dist and s=1/2sum. I would be interested to know if Doniol could do it?
Best wishes
Francis