NavList:

David Pike,

You wrote:

"I once read the difference, 6378:6357, is the order of a postage stamp stuck on a football, but that could just be a such a good story it’s not worth disproving."

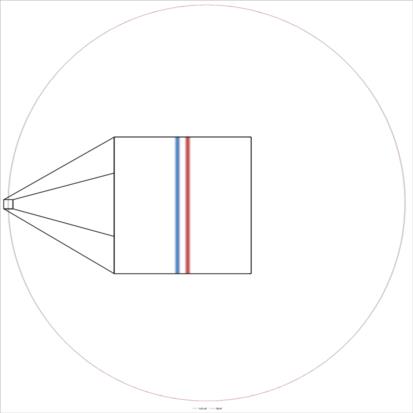
I made the attached image when I was trying to visualize for myself what the difference would look like. If you were comparing the actual radius of Earth with a perfect sphere with a radius matching that of the Earth at the poles (≈6356.8 km), then the inset shows approximately what the difference would look like at the equator. The blue ellipse is the "actual" radius and the red circle is a constant radius. So, I think the analogy you quoted is pretty close to the mark.

Note: To generate this image, I used Excel and the following equation to approximate the radius of the Earth at 1° latitude intervals:

SQRT(((6378.1^2*COS(Lat.))^2+(6356.8^2*SIN(Lat.))^2)/((6378.1*COS(Lat.))^2+(6356.8*SIN(Lat.))^2))

Regards,

Sean C.

File: