NavList:

George Kaplan:

On May 6, I wrote:
"I found an interesting way of writing the relationship between standard dip and dip short. Suppose we call the ratio of distance to sea horizon distance R:
   R = d / d_horizon
For example, at a height of eye of 25 feet, the distance to the standard sea horizon would be 5.8 nautical miles. If an island blocks the sea horizon and is located 2.9 nautical miles away then R is 0.5. We can also express the dip short as a ratio to the standard dip. I'll call that S:
   S = dip_short / dip_horizon.
Note that S is greater than one; if there's an obstruction, the correction we want to apply to an altitude is larger than the standard dip. It turns out that, when you get the factors in the various renditions of the dip short relationship aligned correctly (X and Y above), there's a simple connection between S and R:
   S = (R + 1/R) / 2,
or 
   dip_short = dip_horizon · (R + 1/R) / 2.
I haven't encountered this relationship before, but I like it. Continuing the example above with d_horizon=5.8nm and an island at d=2.9nm, R is 0.5 so S is (0.5+2)/2 or1.25. And since you can calculate the standard dip for any height of eye in your head relatively easily, you can now calculate the dip short in your head. It's simply 25% greater than the standard dip (for R=0.5). So for a height of eye of 16 feet, where the standard sea horizon dip is 4', the dip short would be 5'. If your height of eye is 100 feet, implying standard dip of 9.7', the dip short would still be 25% greater or 12.2'."

When I wrote this up in May for NavList, it was ignored. The idea is, of course, identical to your "Figure 6" in your tech note. I can't emphasize enough that there is enormous practical benefit to this relationship [that I have highlighted in bold above]. The horrible, bullshit formula which has been listed in Bowditch for far too long has grotesquely obscured the simple use of dip short and compelled most navigators to believe that they need a special table or that special "tangent" formula or perhaps that "amateur hour" javascript code from the NGA that I referenced back in May. This (R+1/R)/2 relationship is so much simpler and easy to remember. Better yet, one can picture the graphic (sea below) in one's head relatively easily. In addition, this relationship is independent of first-order variations in ray curvature due to variable temperature profiles (low altitude lapse rate) in the atmosphere.

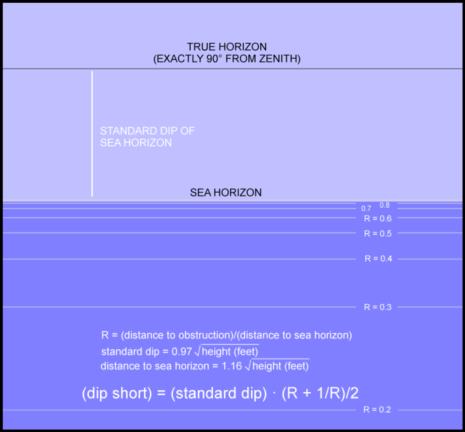
This relationship can be displayed as a "view" toward the horizon with different distances to the "short" horizon displayed just as they would appear visually. I created this graphic back in May, but set it aside then. In the attached "dip short by distance ratio", the gap above the horizon represents the standard "sea horizon dip" for any height of eye. We all know how to calculate that in our heads: it's basically "square root of height of eye in feet" with a factor of 0.97 for slightly better results. We also all know, or should know, that the distance to the sea horizon is the dip "plus a tip" (that's a US reference ...for everyone else it's "dip plus approximately 18-20%"). So if height of eye is 20 feet, that gap in the diagram is 4.3 minutes of arc, and the distance to the horizon is then just about 5.1 nautical miles. The horizontal lines in the graphic below the sea horizon represent various ratios of the dip short distance to the distance to the sea horizon. A ratio of 0.8, for example, means that our foreground horizon (or vessel waterline) is at a distance equal to 80% of the distance to the sea horizon. 

We can use the attached diagram to read off dip short directly, but more importantly it lets us assess sensitivity. Suppose your height of eye is 36 feet. The standard horizon dip is then a little less than 6 minutes of arc, and the distance to the sea horizon would be just about 7 nautical miles. But suppose you can't see the sea horizon. Suppose you have a distant shore that you estimate is 5.5 nautical miles from your location. You can see from the diagram, or you can show by calculation, that the dip short of the horizon in this case differs from the standard dip by less than 0.2 minutes of arc. This isn't even worth consideration. You can use the standard dip and be done with it.

Frank Reed
Clockwork Mapping / ReedNavigation.com
Conanicut Island USA

File: