NavList:

Lars Bergman, you wrote:
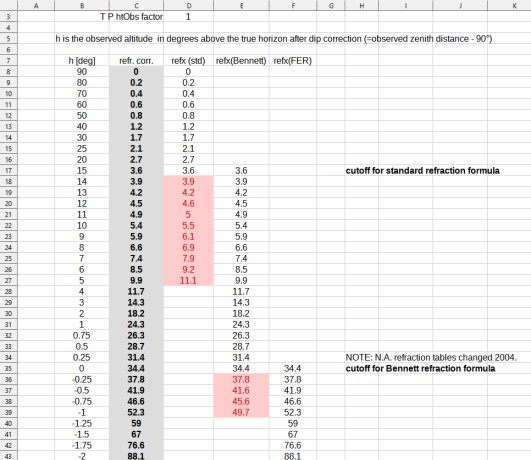
"I have an excel file made at least two years ago giving refraction for negative altitudes. It might be older though. I have a faint memory that it is based on a post by Frank, but I am not sure. Anyway, it calculates R = exp( 3.537 + 0.369 h + 0.051 h² )

Yes, that was mine, and it goes back a wee bit more than two years :) ! Your timing is excellent. I was just re-writing a description of the equation in question, as follows...

SLIGHTLY REVISED FROM A FEW YEARS AGO:
For those who enjoy calculating, here's a short set of general fast formulae (in "code" format, using "*" for multiply, for easy copy and paste; assumes kk is necessary) for refraction covering all observer heights and some angles below the horizon, too:

// angular conversion factor:
kk = 180/pi = 57.2958 [note that most handheld scientific calculators do not require this conversion constant in trig functions (in which case, set kk=1)].
Here h is the angular observed altitude in degrees (corrected for dip).

if h>-3° and h<0°:
// use my new formula below zero degrees altitude (for observers :
  refx = exp(3.537 - .369 * h + .051 * h * h)

if h>0° and h<15°:
// use some variant of the well-known low altitude refraction formula (originally by Bennett):
 refx =  0.998 / tan((h + 7.31 / (h + 4.4)) / kk)

if h>15°:
// use standard high  altitude refraction (this is little more than Snell's Law applied to a constant flat layer of refractive substance):
  refx = 0.972 / tan(h / kk)

// refx as calculated so far is the sea level refraction at standard temperature and pressure of 10° C and 1010 millibars. The result is in minutes of arc.
// Now adjust for non-standard temperature and pressure. TC and P are sea level temperature (but see the last paragraph below) in deg C and pressure in mbar. T is absolute temperature in kelvins.
  T = TC + 273.15
  refx = refx * (P / 1010) * (283.15 / T)

Correction for height above sea level. htObs is the observer's height above sea level in km:
  refx = refx * exp(-htObs / 9.5)

These formulae were validated (by me) with (somewhat time-consuming) integrations using the method outlined in Auer-Standish with an atmospheric model compatible with the refraction tables in the Nautical Almanac (pre-2004), specifically a lapse rate of 7.25° C up to 11km altitude and constant temperature above that altitude. The fit to the integrations is accurate to 0.15 arcminutes or less except in cases where the refraction is relatively large (applying to h<3° or so) in which case the angular error may be a few tenths of a minute of arc but is typically less than 1% of the total refraction. Since red light and blue light from a star have refractions that differ by more than 1% (dispersion), stretching individual star images by an amount larger than the baseline refraction, this error limit should be acceptable in almost every case.

I am including a simple spreadsheet using these three formulae to construct a general refraction table. This table can be directly adjusted for temperature, pressure, and observer height above sea level. Note that in my own code for apps, I use somewhat "evolved" versions of the formulae above, but the differences are usually not significant.

Also note that there are some tricky issues here which I have not addressed. In particular, there is a remarkable physical property of refraction which we take for granted: the refraction at the observer's location depends only and strictly on the temperature and pressure, as measured at the observer's location. We enter our equations or tables with the local T and P. But what about the air a thousand or five thousand meters above you? Don't we need the T and P up there, too? Amazingly, it doesn't matter what's going on in the air above you. Non-standard temperatures and pressures, weird temperature inversions, and more can be present in the atmosphere above the observer but they all distill down to the observable local T and P at the observer's location. That's a wonderful simplifying feature of astronomical refraction. However, this remarkable bit of physics does not apply for light that passes through the atmosphere below the observer's physical altitude --in other words negative angular altitudes. Hence there really should be another weather-related parameter (or more?) in the refraction for negative angular altitudes.

Frank Reed
Clockwork Mapping / ReedNavigation.com
Conanicut Island USA

File: