NavList:

Matus Tejiscak, you wrote:
"In other words, we measure the (two-dimensional) parallax of the Moon very precisely to get our position."

Yes, that's it.

I came upon this idea many lunations ago while thinking about a navigation concept that the late Ken Gebhart of Celestaire had invented. He created a system where a navigator would look at the shape of the setting or rising Sun to determine its altitude in the sky. If the Sun is 5% flattened, that implies a certain altitude. If it's 2% flattened, it's somewhat higher in altitude. The idea is that the refraction depends strongly enough on altitude that we can measure it and then reverse the refraction relation to pull out the altitude. And this eliminates all dependence on the horizon itself being visible. It's a good idea and practical, too, under some interesting circumstances. Refraction has a strong dependence on altitude near the horizon, but it's too small (and corresponds to an overall "scaling" of the sky by about one part in 3000) at high angular altitudes.

The parallax in the altitude of the Moon is similar to refraction. It varies with altitude, and unlike refraction, it remains useful as a test of angular altitude much higher in the sky. If we can measure the Moon's parallax by observing the relative positions of stars above or below the Moon, then we can calculate the Moon's actual altitude above the true horizon from its observed parallax --even when no horizon is visible or available (no sea horizon, no bubble horizon, no horizon at all required).

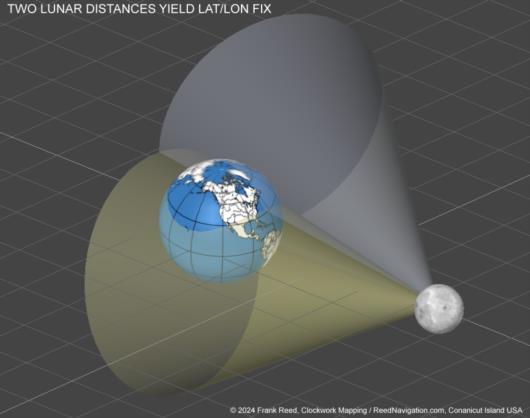
Picture the Moon crossing an observer's meridian at some known UT. We measure the angular distance between the Moon and some star above it, also nearly crossing the meridian. That's a "lunar distance". The measured angle depends directly on the parallax in altitude of the Moon. And that parallax is proportional to the cosine of the Moon's altitude. So from the lunar distance, we can get the Moon's altitude as it crosses the meridian ...and without even once seeing the horizon. Of course the altitude of any known body crossing the meridian at some known time tells us our latitude. So thus we have "latitude by lunar distances". That's worth repeating with emphasis because it should sound odd: "latitude by lunar distances".

Naturally we can extend this to longitude (having nothing really to do with traditional "longitude by lunars") by measuring a second lunar distance that's more or less perpendicular to the first. At known UT a pair of lunar distances gives us a position fix on the Earth's surface. The fix accuracy is approximately sixty times more sensitive to angular error than a common fix by altitudes on the surface of the Earth. Fundamentally, that's because the Moon's mean distance from the Earth is about sixty times the radius of the Earth. Conveniently (or confusingly!) that means that most of our thinking about minutes of arc in standard position fixes can be translated to seconds of arc for position fixes by lunar distance angles. An error of one second of arc yields a position error of one nautical mile on the ground (but see below). Notice then that we need to do all of our work to somewhat better than a second of arc, and that means we have to work with the true limb of the Moon with all its valleys and craters and mountains. This is no longer a problem --apart from the work of implementation. We have detailed, high-accuracy limb profile data from the LRO (Lunar Reconnaissance Orbiter) and a couple of other recent missions.

Geometrically, this "fix" can be understood in terms of "cones of position" extending through space. Each cone has its apex at the Moon's center. As a cone of position extends out into space and passes through the surface of the Moon, the intersections with the lunar surface are circles, entirely analogous to ordinary circles of position in standard celestial navigation. And that makes sense! When I shoot a lunar distance angle, I am measuring an angle between the Moon's limb and the star. But take that observation and imagine moving closer and closer to the Moon until eventually you are in very low orbit above the Moon. The limb of the Moon is now the common "horizon" of the lunar globe, and we see that our "lunar" was actually an altitude measured from the lunar horizon. Even when standing on the Earth's surface looking at the Moon in the sky, the limb of the Moon is the Moon's own horizon, seen at great distance.

In the early days of deep space exploration, like aboard the Apollo moon missions, there were plans to use such observations for real navigation. The Apollo computer had all the math coded to adjust the navigation "vector" based on these deep space "lunars". There was a true, double-reflecting sextant built into the hull (mirrors outside the pressure hull, ocular/eyepiece inside!). By the time of the moon landing missions, this system was already considered redundant, superfluous, and at best an emergency system (which proved out to be of no real value during the only emergency, namely Apollo 13). Navigation updates to the mission "vector" were managed by ground-based observations and calculations. Instead the sextant was used almost exclusively, and, I should add, quite frequently, in a non-sextant mode (like a theodolite), as a type of astro-compass. The astronaut-navigator would ask the computer to point at a specific bright star, like Sirius. The computer would then automatically slew the spacecraft and the sextant so that the star would be visible in the field of view. A little adjustment by the navigator would place the star right on the crosshairs. Then at the press of a button (really a set of keystrokes), the computer would record the new orientation of the spacecraft. These "astro-compass" observations had to be done aboard the spacecraft. There was nothing equivalent that could be managed from the ground. This was a last gasp of manual navigation, even at that level, and within less than a decade relatively automatic star trackers could be used for spacecraft orientation, taking the human navigator out of the loop.

What could we do with this on the ground? The sort of automated "plate solutions" which Paul Hirose brought up have become relatively sophisticated, very fast (in applications that don't try for the "solve all scenarios" approach that astrometry.net adopted), and they are now capable of being coupled with exquisite off-the-shelf digital cameras, like in newer smartphones. If we take photos of stars around the Moon's dark limb and get one arcsecond accuracy in the measured angular positions, it should be possible to get one nautical mile position fix accuracy on the ground on the Earth. Note that this position fix is really a "ray" (the intersection of two cones of position with a common apex at the Moon's center) coming from the Moon's center. This ray has some range of error around it which makes it a sort of "pencil" intersecting the Earth's surface. With one arcsecond accuracy in the work, the thickness of the pencil is about a nautical mile. But we have to remember that this pencil emanates from the position of the Moon in the sky. If the Moon is low in altitude, that pencil's intersection with the ground can be a long narrow ellipse with the long axis pointed at the Moon. The accuracy of the fix is lower in the direction of the Moon's azimuth by a factor of 1/sin(alt). For Moon altitudes above 30°, this is never worse than a factor of two of reduced accuracy in that dimension (towards the Moon's azimuth), but at much lower altitude, it goes up quickly, and renders the fix in that direction too poor to be useful for Moon altitudes below about 5°. The accuracy of the fix in the direction perpendicular to the Moon's azimuth is not affected.

By the way, I wrote all this up nearly twenty years in online posts and gave a presentation on it at the NMM in Greenwich twelve years ago. It's conceivable that someone has tried to patent this methodology. Patents could be a problem for an app or other implementation, but my posts and presentation may reduce the impact of any such patents.

Frank Reed
Clockwork Mapping / ReedNavigation.com
Conanicut Island USA

PS: What can we achieve without digital imaging? The geometric solution does not require digital imaging. Averaging multiple observations with a good metal sextant can get us close to 0.1' or 6 seconds of arc so that would imply six nautical miles accuracy in a fix for latitude and longitude, with the limitations described above. But even in this case, we are close to the limits of analysis tools than are now available, including my own, since they do not incorporate the true shape of the Moon's limb.

File: