NavList:

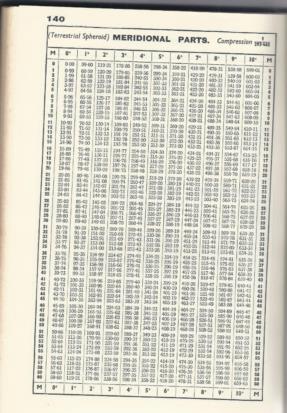
The Mercator projection employs the simplest form of integration (in the calculus sense) of local conformality to produce a global projection. Indeed, the mathematical equation which defines the Mercator projections y-values, also known as meridional parts, is nothing more than the integration of the differential relationship dm = dlat / cos(lat). That is, if you take the local scaling factor, cos(lat), which provides local conformality, and then extend it from one central latitude to the next, advancing steadily up the chart in latitude in arbitrarily tiny steps, the cumulative values of the y-coordinates on the chart are the integral of 1/cos(lat) which is, among other equivalent forms, log[tan(45°+lat/2)]. This defines the global Mercator projection.

Thanks for being persistant (I think I have seen this subject discussed several times in the archives). I think I finally understand it.

• A conformal map preserves angles locally.
• A mercator projection has a variable lat/long scale based on meridional parts. It is locally conformal.
• Projections other than mercator may be locally conformal.

If I draw a plotting chart with a long = cos(fixed lat) scale I have drawn a locally conformal (but not Mercator) chart.

If I open Norie at the Meridional Parts table and create a chart with a long proportional to (difference meridional parts) scale I have drawn a Mercator chart. This chart is conformal.

Here is a 1958 plotting chart drawn on the Mercator projection. Presumably if I measured  the long scale it would change with latitude? I chose this chart because in the west there is a very small island which, according to the legend at bottom of the chart, may be several miles out of position.

https://ndhadeliver.natlib.govt.nz/delivery/DeliveryManagerServlet?dps_pid=IE21794248

File: