NavList:
A Community Devoted to the Preservation and Practice of Celestial Navigation and Other Methods of Traditional Wayfinding
From: Robin Stuart
Date: 2017 Apr 6, 12:48 -0700
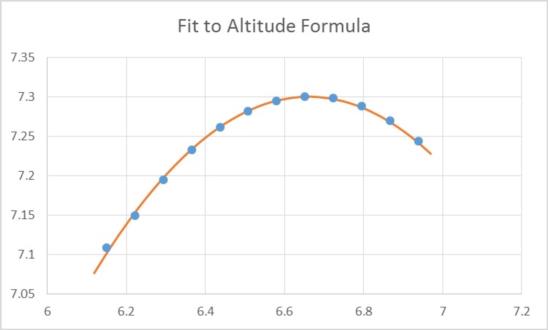
I improved on my rough and ready quadratic fitting calculation with a more rigorous approach. First each observation is corrected by its own corresponding refraction and parallax correction plus semi-diameter (dip=0). Then using the standard altitude with linear time-dependence in GHA and declination
sin H0 = sin L sin(δ0 + d/60 ΔT) + cos L cos(δ0 + d/60 ΔT) cos( GHA0 + λ + 15 ΔT )
where GHA0, δ0 are the GHA and declination at some convenient time, T0, and ΔT = UT - T0.
After an initial estimate of the latitude, L, and longitude, λ, you can calculate the sum of squares of differences between the formula and observations and then obtain the least squares fit to L and λbut numerical methods. This approach has a number of advantages
1) The fit is logically correct and doesn’t rely on the assumption that the altitude as a function of time approximates a parabola. It should therefore work even when the Sun transits at a high altitude or the observations are taken over quite a long time interval. In principle the observations don’t even need to bracket noon.
2) It’s a 2 parameter fit rather than 3 in the case of the quadratic
3) No need for the equation of time or a correction for the difference between LAN and time of maximum altitude. It’s all automatically incorporated in the fit
This method is equivalent to the multi-LoP method given in the Nautical Almanac but without the locally flat Earth approximation. You immediately get don’t get the time of maximum but you don’t need it.
The answer I get is 66°25.4′S 81°37.8ʹE which is on the coast Mikhaylov Island.
Just for fun I applied this approach to the observations at 6:30:30 UT and earlier only. I get 66°25.6′S 81°44.5ʹE
Robin Stuart