NavList:
A Community Devoted to the Preservation and Practice of Celestial Navigation and Other Methods of Traditional Wayfinding
From: Frank Reed
Date: 2022 Oct 17, 07:33 -0700
I created two "Vertical Lunar" test cases yesterday for my own analysis. Some of you may find uses for them, too, so I'm sharing the details. I have placed our imaginary observer near the equator and near the Galapagos Islands for "round numbers" on the latitude and longitude. Height of eye for both scenarios is 17 feet, implying dip is 4.0'. Assume standard temperature and pressure conditions and zero index error. Each lunar observation consists of one carefully measured lunar distance as well as less carefully measured altitudes of the Sun and Moon taken simultaneous with the lunar distance. By design there is no significant error in the "observed" inputs. In both cases the Moon and Sun are on opposite azimuths, and therefore the Moon's bright limb is necessarily pointing up and the Moon altitude must be UL. The Sun altitude is, as it almost always is, LL.
Vertical Lunar I:
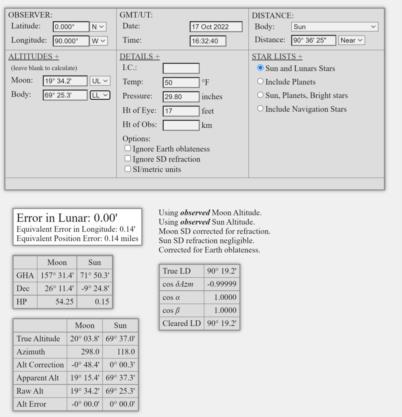
Latitude: 0.000°, Longitude: 90.000°W (among the Galapagos, some island peaks possibly visible)
Date/Time: 17 Oct 2022 at 16:32:40 UT
Moon altitude: 19°34.2', Sun altitude: 69°25.3'
Observed Lunar Angle: 90°36.4'
Vertical Lunar II:
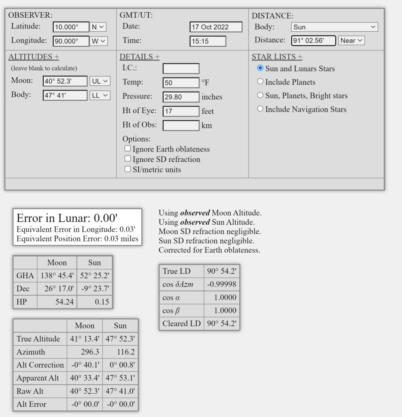
Latitude: 10.000°, Longitude: 90.000°W (about 350n.m. west of San Jose, Costa Rica)
Date/Time: 17 Oct 2022 at 15:15:00 UT
Moon altitude: 40°52.3', Sun altitude: 47°41.0'
Observed Lunar Angle: 91°02.6'
Your challenge: determine UT by computation, either by a "vertical lunar" approach, which is fast and useful for learning, or by any favorite clearing method you may have (does a vertical lunar create any special issues for your favorite standard clearing method)? How does the computed UT compare with the given time in the setup of each scenario? Note: you don't have to take this challenge literally! Find whatever use you like in these scenarios. But there are definitely interesting issues to discover by working these cases as in the challenge. :) I'm attaching standard results from my online clearing app which you can use for reference. The additional precision in the distances seen there is not relevant --just evidence of my own experimentation.
Frank Reed
Coming soon: my online workshops in LUNARS covering big history, practical history, modern practice, and math, too.
Two session options in November. Details here.