NavList:
A Community Devoted to the Preservation and Practice of Celestial Navigation and Other Methods of Traditional Wayfinding
From: Robert H. van Gent
Date: 2022 Mar 5, 11:19 +0000
Hi,
The table looks fine to me, I see no numerical errors.
The left and the right tabular values all add up to 89d 60m (or 90d 00m), as they of course all should.
rvg
From: NavList@navlist.net <NavList@navlist.net>
On Behalf Of Noell Wilson
Sent: 04 March 2022 21:15
To: Gent, R.H. van (Rob) <R.H.vanGent@uu.nl>
Subject: [NavList] W. & S. Jones Helborn, London box sextant tangent table
I’ve been trying to figure out what I thought was the tangent table engraved on the back of a W. & S. Jones Helborn, London box sextant.
At first glance it’s different so it took a while. Then, I’m pretty sure, it has two errors so it took a longer time.
It’s pretty clever in its simplicity and economy of engraving.
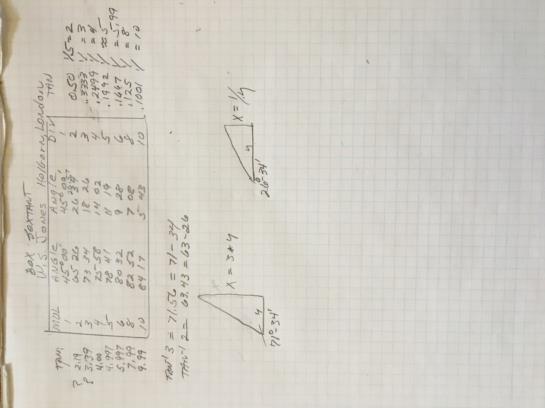
First, the Tangent table would probably be used for measuring, or calculating, things on the ground. You’d measure a base distance and then use the tangent table to find the unknown distance.
Instead of giving you a tangent table at regular intervals, this one gives a few regular tangents and you would set that angle on your sextant and move until the images on the sextant matched.
The outlined part of the attached worksheet is what’s engraved on the sextant. Everything outside of that is my notes.
On the left side - the angles above 45 degrees - 75 degrees 58 minutes has a tangent very close to 4.
So, if you were calculating the height of a tree, you’d set the sextant to 75d 58m and find a spot where the top and bottom images of the tree matched. Then your distance from the bottom of the tree (level ground, right angles, everything ideal) times 4 would
be the height of the tree.
The right side of the table -angles less than 45 degrees - is the clever part. To keep from engraving long decimal fractions, the tangent is 1/over the numbers listed under “DIV”.
So if the layout favored an angle of 18d 26m, you’d set that and move until both ends of the unknown object matched up in the sextant. You’d then divide your distance from the base of the object by 3 to get the unknown distance. With the sextant set at 18d26s
and a distance from the base of 100 feet, the unknown distance is 100/3 or 33.3 feet. This kept them from engraving .333 in the table.
Now, the errors. On the left side, I think the angles corresponding to a tangent value of 2 and 3 should be 63d 34m and 71d 34m respectively. (If I had never written anything in error, I’d make fun of the engraver or the mathematician.
As it is, I’m just hoping I didn’t mess up a word or number here.)
Regards, Noell