NavList:

Ed Popko, you wrote:
"In response to Doug's question about estimation of sun's declination, you suggested a simple graph would produce better results than a linear interpolation between solstices. Is the attached drawing close to what you were suggesting?"

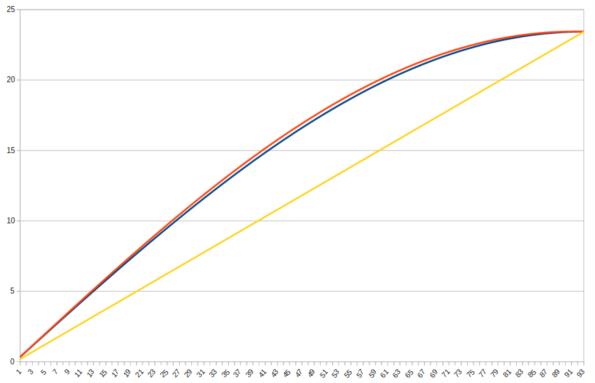
Yes, that's it. Note that a graph of the Sun's declination versus date closely resembles a sine curve (see the image). So by drawing a quadrant of a circle, labelling evenly-spaced points around the circumference of the quadrant with the dates from equinox to solstice, and then projecting onto the vertical axis, we are simply generating sine values with a graphical method. It's not perfect since the graph of Dec versus date isn't quite a sine curve. You can expect about a quarter of a degree error from the approximation which is probably also close to the limit for what you can read from a diagram like this.

I'm including a graph showing the Sun's Dec from March 21 to June 21 next year, as well as a simple sine approximation and a linear interpolation. The actual declination is the blue curve. The sine approximation is the red curve. The linear interpolation is the yellow line. The sine approximation is out by a maximum of 0.3°. The linear interpolation is wrong by a maximum of 4.9°.

For a "what if" scenario, how would the curves compare if the obliquity of the ecliptic were 85° instead of 23.44°??

I mentioned another concern in a previous reply. You don't know the exact instant of the equinox, and this could throw off you Dec in the months near the equinox by another quarter of a degree or so. But in a "closer to the real world" case, this wouldn't necessarily be an issue. If you have been navigating using the Sun on a more of less daily basis, and you lose your almanac date source somehow, you can probably find a recent correct value in your notes. Also, near the equinoxes, if you do it right, a linear approximation works quite well. In fact, if you lost the almanac overboard on Sep. 2, let's say, but you have your Dec from that date and just work under the assumption that the Dec decreases at a constant rate to 0°00' on Sep. 23, then you'll do fine well into October, maybe out by 0.3° by Oct. 10. Nearly six weeks with a linear approximation is pretty good.

Frank Reed

File: