NavList:
A Community Devoted to the Preservation and Practice of Celestial Navigation and Other Methods of Traditional Wayfinding
From: David Pike
Date: 2015 Jan 1, 06:29 -0800
Francis, Mike. The link is a very good article. I seem to remember top of the range ex-Warsaw Pact station pointers being advertised on eBay a couple of decades ago at reasonable prices. However, you don’t really need one. In the RAF we used what might be called the ‘greaseproof paper method’ for scoring PPI radar pictures of limited aids navigation exercises and simulated bomb releases. Take a PPI radar photograph at the release point, and identify three radar significant points approximately 120° apart. Mark also the centre of the radar picture. Then take a piece of best quality RAF tracing paper (draftsmen, chefs, and aircrew for the use of – it used to come in huge rolls, but greaseproof paper would do). Place the paper over the photograph and draw lines from the centre of the photograph to the three radar significant points and extend the lines. Place the paper over a 1:63,000 (in those days) Ordnance Survey Map. Wiggle it around until the lines fit over the points on the map. The point you’ve drawn the lines from is now over the place you were when you took the photograph (give or take a couple of hundred yards, because nothing’s perfect – always a point of argument between the crew and the assessor).
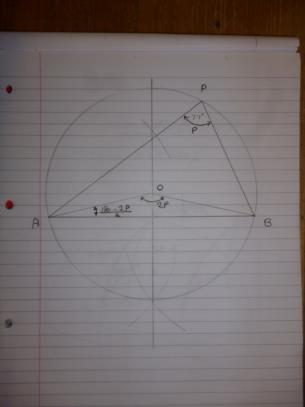
The circles method described in the article is also quite good. Going back to the few hours frantic revision I did before my Maths ‘O’ Levels in 1960, it all depends upon three facts from the geometry of circles namely: a. The angle subtended on the circumference of a circle from a chord is the same at any point. b. The angle subtended at the centre of a circle from a chord is twice the angle subtended at the circumference. c. The centre of a circle lies on the perpendicular bisector of a chord. Plus the angles of a triangle add up to 180°, and the opposite angles of an isosceles triangle are equal. So in the diagram below, AOP = 2xAPB° and OAB = OBA = 180° – 2P = 90°-P. Therefore, join A to B; construct the perpendicular bisector; draw a line at 90·-APB to AB. Where this line crosses the perpendicular bisector of AB is the centre of the circumscribing circle upon which P must lie. Do the same for BC. Where the two circles cross is P. It's funny how I can remember that but not what day it is. Dave