NavList:

I had written:

"I get it from figure 4 that the spacing of the additional lines is proportional to the lengths of the sides (LOPs) making up the cocked hat. But just knowing that doesn't tell you what spacing to use since many spacings will satisfy the proportion."

see:
http://www.navlist.net/m2.aspx?i=114965&y=201012

----------------------------------------------------------------------------------------------------------

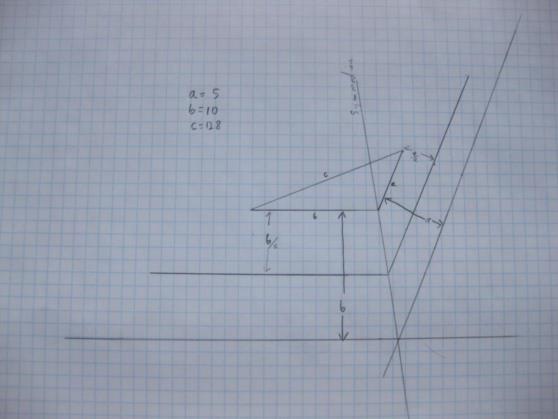
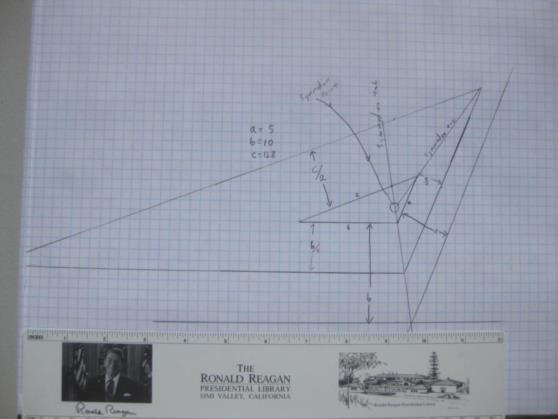
I now understand that all you need to know is the proportions between the sides in order to determine the symmedian line. This line is determined by connecting the vertex of the original cocked hat with the vertex of the larger triangle that you construct around it with the sides spaced proportional to the lengths of the respective sides. You end up with the same symmedian line no matter what spacing you use as long you maintain the correct proportions. I have attached two diagrams to illustrate this. The first diagram shows the construction for the vertex of a and b with the lines spaced equal to sides a and b and also with them spaced at a/2 and b/2 and you get same symmedian line. The second diagrams show the construction for the symmedian for the vertex of a and c with the lines spaced at a/2 and c/2. The intersection of the two symmedian lines determine the symmedian point. This diagram also illustrates the problem with this method of constructing the symmedian point, the enclosing triangles can get pretty big pretty quick and might run off the paper.

So, we have three ways of finding the symmedian point, 1) construct the medians and the bisectors, measure the angle between them, and then construct the symmedian lines by drawing the lines at the same angle on the other side of the bisector. 2) Greg's method involving drawing the same first two lines and then using a drawing compass to determine where to draw in the final lines. And 3) the method advocated by Herbert which I have just illustrated.

In my opinion, all three constructions are difficult and time consuming and do not provide a point with a greatly greater probability than the other methods of selecting a point to use for the fix, the centroid, the incenter and the steiner point. Of these methods it appears that the steiner point comes closest to approximating the symmedian point and is extremely easy to use. (And, of course, there is also the eyeball method.

See:

http://www.navlist.net/m2.aspx?i=114770&y=201012

http://www.navlist.net/m2.aspx?i=114970&y=201012

gl

----------------------------------------------------------------
NavList message boards and member settings: www.navlist.net/NavList
Members may optionally receive posts by email.
To cancel email delivery, send a message to NoMail[at]navlist.net
----------------------------------------------------------------