NavList:

   

Reply

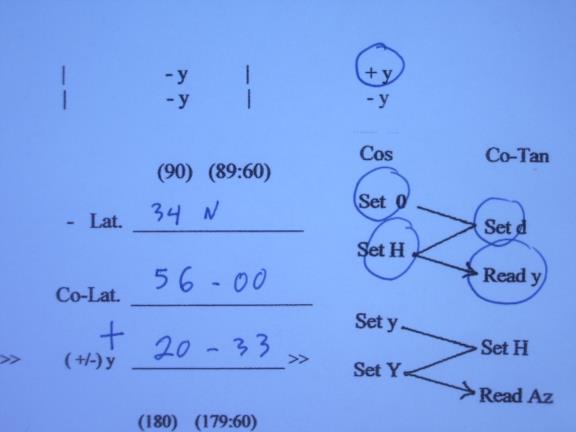
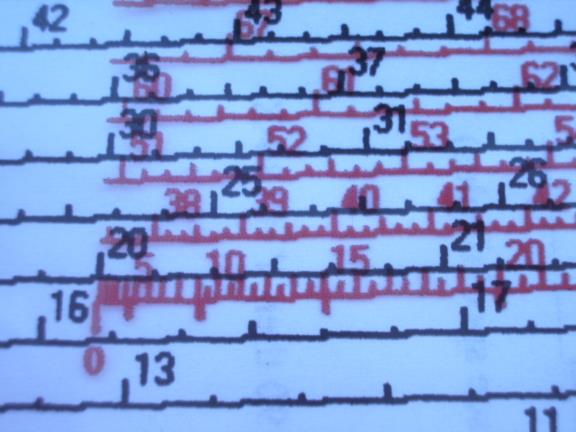
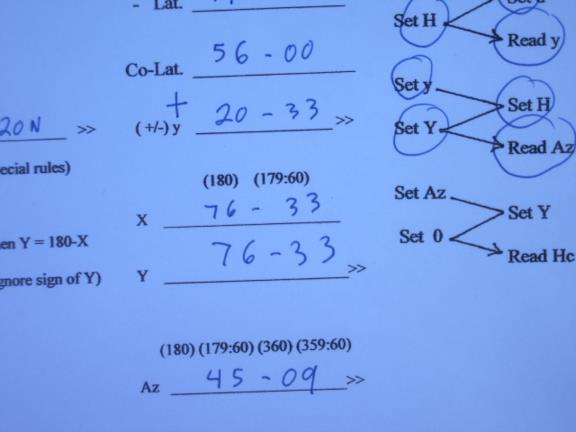
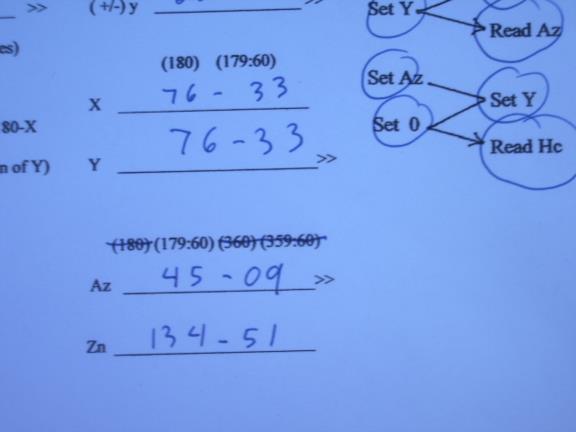
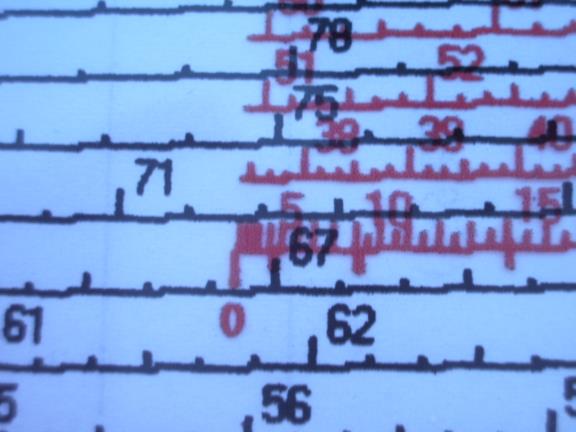
There are often posts on the Navlist regarding using celestial as a backup to 
GPS and finding a simple way to do this. I think I have found a method that 
is simple, self contained, takes up little space, needs no almanac or sight 
reduction tables and requires no batteries. This method is meant for those 
who already know celestial navigation and provides a very compact and 
self-contained system needing no books, almanacs or tables.

The first part of the kit is simply the long term almanac from H.O. 249 along 
with the Polaris tables and the Precession & Nutation  table to allow the use 
of the tabulated coordinates for the stars for a long period of time. Since 
this almanac only covers the sun and the stars no provision is made for 
handling planets or the moon but that is not that important for a "backup" 
celestial method.. However, if you have the Nautical Almanac then you can 
work with these bodies as well. I have included a form to use with the long 
term almanac which also includes  tables for correction of observations. The 
long term almanac consists of nine pages from H.O. 249 plus a computation 
form which can be printed back to back on only five sheets of paper.

The main part of this method relies on my adaptation of the long extinct 
Bygrave slide Rule which is elegant in its simplicity but which produces 
altitudes and azimuths within in one or two minutes of arc and takes less 
than two minutes to do the computation. I have included three PDF files that 
can be printed out to create a working copy of my adaptation which consists 
of three  sheets containing the modified scales which can be hole punched and 
kept in a thin three ring binder (or in an envelope) with the long term 
almanac and extra forms for recording the computation. The Cotangent scale 
should be printed out on paper and can be sealed in a plastic sheet for good 
durability. The Cosine scale and the Vernier are printed out on plastic 
transparency sheets in an inkjet printer and can also be sealed in additional 
plastic sheets for durability. The entire backup method is contained on a 
total of only eight sheets, five for the almanac and three for the Bygrave 
slide rule!

When using the Bygrave slide rule the azimuth and altitude are calculated in 
three steps using the same manipulations of the slide rule for each step. I 
will first describe the use of the normal cylindrical Bygrave slide rule 
which utilizes a cursor or pointers to align the scales. I have also enclosed 
a copy of the original Bygrave instruction book. The Bygrave has also been 
discussed on the Navlist.

We first calculate the intermediate value "y" (lower case y)  which is found by the formula:

tan y =  tan declination / cos H          (H = Hour angle)

This is the formula listed in the Bygrave manual but, in fact, the slide rule 
does the calculation by modifying this formula to allow the use of the 
cotangent scale. The actual manipulation of the slide rule uses the 
re-arranged formula of:

cotan y  =  cotan declination x cos H

You accomplish this computation by setting one of the pointers (or the cursor 
on my copy) to zero on the cosine scale and while holding it there rotate the 
cosine scale and slide it up or down on the cotangent scale so that the other 
pointer (or cursor) is aligned with the declination on the cotangent scale. 
Now, holding the cosine scale still, rotate the pointer (cursor) to point at 
the hour angle (H) on the cosine scale and then read out "y" from the other 
pointer (cursor) where it points on the cotangent scale.

Next you find the second intermediate value,"Y" (upper case Y) by adding "y" 
to co-latitude (if latitude and declination have the same name) or by 
subtracting "y" from co-latitude (if of opposite names.)

[I kept the original nomenclature from Bygrave so that the original literature 
can be followed . I think it is confusing to use the same letter of the 
alphabet for two variables, "y" lower case y, and "Y" upper case Y, and I 
don't know why Bygrave chose this system. I prefer to replace "y" with "W" in 
the formulas and have done so on my forms.]

Next we find azimuth with the formula :

tan Az  =  (tan H x cos y ) /  cos Y

which is re-arranged into the form:

cot  Az = (cotan H / cos y  ) x cos Y

Using the same manipulations as before, set one pointer to "y" on the cosine 
scale and the other pointer on H on the cotangent scale, move the cursor to 
"Y" on the cosine scale and read out azimuth from the other pointer on the 
cotangent scale.

The third step calculates altitude, Hc. using the formula:

tan Hc = cos Az x tan Y

with the formula re-arranged into the form:

cot  Hc  = cot Y / cos Az

set one pointer to Az on the cosine scale with the other pointer to "Y" on the 
cotangent scale. move the pointer to zero on the cosine scale and read out Hc 
from the other pointer on the cotangent scale.

I have developed an even simpler implementation of the Bygrave, one that is 
very easy to make since it doesn't require concentric tubes. I made this by 
printing out the cotangent scale twice on a piece of paper. I then printed 
the cosine scale in red on a transparent sheet so that the cosine scale can 
be placed directly on top of the cotangent scale and aligned much like a 
normal slide rule. We follow the same steps as already described but it is 
even simpler since no cursor needs to be used. I will illustrate how easy it 
is to use with an example. I have include a form and pictures of the scales 
showing this computation.

Since the Bygrave doesn't require that the latitude or the LHA to be whole 
degrees  you can compute Hc for your D.R. position but for convenience in 
this example we will use 34� N for latitude, for declination, 14� N and the 
LHA is 346�.

Look at illustration number 1 (i.jpg) which shows the form to be used with 
this simplified model of the Bygrave. The top of the form is used to compute 
hour angle, "H", in the range of 0� through 90�. You enter the LHA in the 
proper column and make the computation. You can see in our example we have 
placed the LHA, 346�, in the column for LHAs in the range of 270� to 360�. 
The form shows that in this case we subtract LHA from 360� to find "H", hour 
angle, in this example, 14�.  We have carried this 14� down to the "H" blank 
on the form and we have entered declination and latitude in the appropriate 
blanks.(2.jpg)

[The scales on the original Bygrave ran from 20' up to 89� 40' and then back 
in the reverse direction from 90�20' to 179�40'. My simplified version 
eliminates the second set of numbers keeping the scale less cluttered. The 
original Bygrave allowed hour angles of 0� to 180� east and west (which had 
been normal celestial practice prior to the introduction of the concept of 
LHA) but because my version eliminated the second set of numbering on the 
scales it is necessary to get hour angle, "H", into the range of 0� and 90� 
which is accomplished on the top part of the form. Other changes were also 
necessary because of my simplification of the scales and they will be pointed 
out later.]


(To avoid confusion I have switched to using "W" to replace Captain Bygrave's lower case "y.")

Next we subtract the latitude from 90� to form co-latitude. If we were using 
our D.R. latitude we would subtract it from 89� 60' since this notation makes 
it easy to subtract degrees and minutes. In our example the co-latitude is 
56�. We use the top of the form to determine if we will be adding or 
subtracting the intermediate value of "W" to co-latitude. This is determined 
by the column of the LHA and by the names of the latitude and declination. In 
our example we can see that we will be adding "W" since LHA is in the last 
column and the names of the latitude and the declination are the same. Just 
circle the "+" mark at the bottom of this column and also place a "+" mark on 
the "W" line under the co-latitude line.(3,4 and 5.jpg)

[With the original Bygrave you always added if latitude and declination had 
the same name and subtracted if of opposite names. Because of my simplified 
scales you must subtract "W" if same name and LHA between 90� and 270�, and 
the form accomplishes this. This puts you at exactly the same place on the 
scales as with the original Bygrave. You still always subtract if of opposite 
names.]

Next we will follow the zig-zag diagram along the right edge of the form to 
find the value of "W". The left side of the zig-zag indicates the cosine 
scale and the right side indicates the cotangent scale. The same process is 
used three times and values are always taken off from the cotangent scale, 
never from the cosine scale. The zig-zag tells us to line up 0 (zero) on the 
red cosine scale with "D" (declination) on the black cotangent scale. We then 
look at "H" (hour angle) on the red scale and take out "W" from the adjacent 
cotangent scale. (6.jpg)

On both scales the numbering is above and to the right of the marks on the 
scales. I have aligned the red cosine scale slightly below the black 
cotangent scale for clarity. We can see that the red zero is lined up 
directly below the black tick mark for 20� (the declination). You usually use 
visual interpolation for the minutes of declination. Now, without allowing 
the scales to shift, we locate "H" on the red scale and read out "W" from the 
adjacent black scale, in this case 20� 33', and write this value on the "W" 
line below the co-latitude. (7.jpg)

Next we find he second intermediate value, "Y", by first determining "X" by 
adding "W" to co-latitude, in this example "X" = 76� 33'. Then, following the 
rule on the form, since "X" < 90 then "Y" = "X" and we carry it down to the 
"Y" line. If "X" > 90 we would subtract "X" from 180� (or from 179-60) to 
form "Y".
[I introduced this new intermediate variable "X" so that the resulting "Y" 
will be less than 90� which allowed me to keep the scales less cluttered 
since the reverse numbering, 90�20' to 179� 40', found on the original 
Bygrave is not needed.](8 and 9.jpg)

We now follow the second zig-zag to find Az . (Note we start with the value 
computed at the last step, "W.") (10.jpg) Using  the same manipulation as the 
first time, we line up "W" on the red scale with "H" on the black scale . We 
than look at "Y" on the red scale and take out Az from the adjacent black 
scale. Looking at illustration 11 (11.jpg), we have lined up red 20-33 with 
black 14 by aligning the 20-30 mark slightly to the left of the "14" on the 
cotangent scale. (Remember at this point on the red scale the short tick 
marks show 1/2 degree or 30'.) Next we located "Y" on the red scale (76-33) 
and take out the Az from the black scale. (12.jpg) (The red 76-30 mark is 
lightly to the left of the black 45 tick mark and the red 76-40 is aligned 
with the black 45-20 so by visual interpolation the red 76-33 will align with 
the black 45-09, the Az. (At this point on the scales each tick mark is 10'.)

Next enter the Az on the form  and compute Zn by applying the rules on the 
attached form, in this case the celestial body is to the south east so we 
subtract Az from 180� (179-60) to determine Zn, 134� 51' (or 134.9�).(13.jpg)

[Because of my simplified scales the determination of Zn is different than 
with the original Bygrave since you can only read out Az  in the range of 0� 
to 90� with my version while on the original Bygrave the Az was taken out in 
the range of 0� to 180�. The determination of Zn is usually not a problem in 
real life since you know the approximate direction of the body when you take 
the sight. I have include rules to resolve any ambiguity.]

We now follow the last zig-zag to calculate Hc. ( Note we again start with the 
value computed at the last step, Az). (14.jpg) Using the same manipulation as 
before, we line up Az on the red scale with "Y" on the black scale.  Next we 
locate zero on the red scale and take out the Hc from the adjacent black 
scale. Looking at no. 15 (15.jpg) we see that we have aligned he red 45 tick 
mark slightly to the right of the black 76-30 (each tick mark is 10' on both 
scales) and we visually interpolate red 45-09 with black 76-33. Looking now 
at no. 16 16.jpg), we find the red zero and interpolate on the black scale to 
take out the Hc of 71� 17'and enter it on the form. (17.jpg)


Comparing our result with H.O. 249 (see no. 18, 18.jpg) we find the Hc in H.O 
249 of 71� 17' and Zn of 135�, the same as with the Bygrave.

The original Bygrave had a cotangent scale marked every one minute of arc 
while the cotangent scale of my reproduction is marked every ten minutes and 
in some cases every five minutes. The original cosine scale was marked at 
varying spacing and my recreation is also, but not as frequently as on the 
original. At most places on these scales it is sufficiently accurate to 
visually interpolate. However, at places where the scale markings are far 
apart, visual interpolation is not accurate enough. To improve the accuracy 
of my reproduction I have added a scale that assists in interpolation. This 
scale consists of a small diagram with converging numbered lines and should 
be used on the cosine scale above 80� and on the cotangent scale above 80� 
and below 10�. To use it slide it up until the outside lines, labeled zero 
and ten, fit between two marks on the main scales and then use the 
intermediate lines for the interpolation. In most cases it is not necessary 
to use this vernier. If the scales were more finely divided this Vernier 
could be dispensed with completely.


There are some unusual cases that require slightly different procedures and 
all of these special cases are described on the form. If "H" is less than 1� 
or greater than 89� (actually 89� 15' on my version) simply assume a 
longitude to bring "H" within the range of the scales. The intercept will be 
longer but perfectly usable for practical navigation.

If the computed azimuth is greater than 85� the computed altitude will lose 
accuracy even though the Az is accurate. For azimuths in this range even 
rounding the azimuth up or down one half minute can change the Hc by ten 
minutes. So you use the azimuth but you compute altitude by interchanging 
declination and latitude and then doing the normal computation. You discard 
the azimuth derived during the computation of altitude and use the original 
azimuth.

When declination is less than 55' on my version (less than 20' on the 
original) you can't compute "W" because you start the process with 
declination on the cotangent scale. In this case, Bygrave says to use the 
same process as when the azimuth exceeds 85�, you simply interchange 
declination and latitude and compute altitude. But Bygrave didn't tell us how 
to calculate azimuth in this case. In my testing I have found a method that  
produces quite accurate azimuths. You simply skip the computation of "W" and 
simply set "W" equal to declination. The  worst case I have found is that the 
azimuth is within 0.9� of the true azimuth but most are much closer. If the 
declination is less than one degree and the latitude is also less than one 
degree, follow this procedure and also assume a latitude equal to one degree. 
After you have computed the Az you then follow the same procedure discussed 
above for azimuths exceeding 85� by interchanging the latitude and 
declination and then computing  Hc.

Another rare possibility is that "Y" will exceed 89� 15' after adding "W" to 
co-declination so it won't fit on the scale. The simple way to handle this 
situation is to assume a latitude so the "Y" does fit on the scale even 
though the resulting intercept is longer but still usable.

An extremely unlikely case (I only mention it to be complete) is that "W" 
exceeds the range of the cotangent scale, 89�15', so cannot be computed in 
the first step of the process.  This can only happen when shooting one star, 
Kochab, which has a declination of 74�13' north and then only if "H" exceeds 
87� 20', an extremely unlikely event.

I am attaching a revised form to use with the Bygrave slide rule. This form 
steps you through the computation and contains
 the rules for the special cases. The special cases are likely to come up only very rarely in practice.

 The first rule for H < 1� or H > 89� only involves LHAs covering 4 degrees 
out of 360� (LHA in the ranges of 0 -1, 89-91, 269-271, and 359-360) so only 
occurs by chance very rarely and these can be avoided if sights are 
preplanned as is the normal procedure for flight navigation. Worst case, you 
have to change the time of the observation by four minutes.


Rule 3 covers the case when Y exceeds 89� which covers a range of two degrees 
out of a possible 180� so is also very rare. Co-lat is in the range of 0-90 
and W is also in the same range so X comes in the range of 0 -180. If X is 
less than 89 then Y is also less than 89. If X is greater than 91 then Y is 
less than 89 also. Only in the case of X between 89 and 91 will Y exceed 89. 
This situation can't be avoided in advance because you can't predict what the 
value of W will be but just assuming a latitude that differs by one degree 
solves the problem which will result in a longer intercept but one that is 
still usable.

The fourth rule deals with cases of bodies bearing almost directly east or 
west and this situation can be avoided by choosing a different body to shoot 
or, if only the sun is available,by waiting a few minutes to allow the 
azimuth to change out of this range.

The remaining situation covered by rule two (declinations less than one 
degree) concerns only bodies in the solar system since none of the 
navigational stars have declinations less than one degree. Obviously the most 
important body is the sun and its declination is between 1� north and 1� 
south for five days in March and again in September so this situation can't 
be avoided and this is the most important special case. The special rule 
handles it nicely and the Hc is completely accurate. The computed azimuth is 
an approximation but is never more than one degree different than the actual 
azimuth and is usually much closer. Since you can use your D.R. for the A.P. 
the intercepts are short and this slight inaccuracy in the azimuth will not 
make a noticeable difference in the LOP.


So give it a try and let me know what you think.

Gary J. LaPook

File: 



File: 



File: 



File: 



File: 



File: 



File: 



File: 



File: 



File: 



File: 



File: 



File: 



File: 



File: 



File: 



File: 



File: 

   

File: 

   

File: 

   

File: 

   

File: 

   

File: 

   

File: 

   



--~--~---------~--~----~------------~-------~--~----~
Navigation List archive: www.fer3.com/arc
To post, email NavList@fer3.com
To , email NavList-@fer3.com
-~----------~----~----~----~------~----~------~--~---

   

Reply