NavList:
A Community Devoted to the Preservation and Practice of Celestial Navigation and Other Methods of Traditional Wayfinding
From: Frank Reed
Date: 2019 Dec 14, 10:10 -0800
Antoine C wrote:
"Let us first define a "Geocentric Fictitious Sun" as follows :
Fictitious Sun RA = Apparent Sun RA + 180°
Fictitious Sun Dec = Opposite of Apparent Sun Dec
Fictitious Sun Distance = Equal to Sun Distance.
We can then define "Full Moon" as being the time of minimum geocentric distance between apparent Moon Center and Fictitious Sun Center."
This is un-necessary mathematically though it may help with visualization. This is equivalent to finding the great circle distance on the globe to a target point nearly antipodal from the starting location by examining the distance from the actual antipode to the target point. The math doesn't care, but if you try it on a globe, it's easier to look at the antipode point. Those two distances (starting point to target point, and antipode to target point) add up to 180° exactly. The distance from your "fictitious Sun" to actual geocentric Sun is 180° exactly. Minimizing the angle from the fictitious geocentric Sun to the geocentric Moon is mathematically identical to minimizing the angular distance (the "plain old" Lunar Distance, LD) from the geocentric Sun to the geocentric Moon.
And Antoine added:
"This is not the official definition, but it is at least as good as the official one since it does have a meaningful and solid physical sense and since it also does NOT depend on the coordinates system being used for such computation."
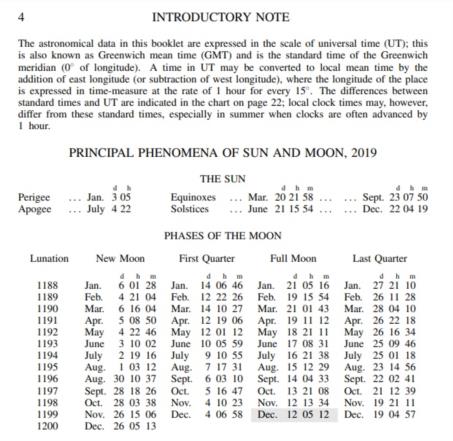
As I noted in my prior reply, the standard "official" definition of the Moon's phases is governed by geocentric ecliptic longitude (or at least appears to be). This is the standard used by various standard almanacs (see the page from the official publication "Astronomical Phenomena for 2019" below). By the standard definition, the Moon is Full when the difference in geocentric ecliptic longitude is 180°. This happened at 05:12 UT which was 12:12 EST just as the various "whaddaya know" memes stated ("Full Moon at 12:12 on 12-12?? Whaddaya know?!"). Never mind that no observer actually saw that phase at that time (since it's defined geocentrically) and never mind that this is just a quirk of zone time and it was only "12:12" in EST. Numerological memese like these are built on cute coincidences that imply some sort of "good luck" for folks weaned on lottery tickets and slot machines.
Separately, outside the official definition, we can define Full Moon as absolute maximum phase or "full-ness" which is identical to the maximum Sun-Moon lunar distance, LD, since the phase is equal to (1-cos LD)/2, which, for those of you who get a kick out of haversines, is the same as phase=hav(LD). As I noted in my earlier reply, the max geocentric Sun-Moon LD occurs at 12:30 (12:31 is not inconsistent).
I agree that this definition in terms of actual phase is more natural, but it's too late to make changes. Official government-issue astronomical sources have been using the ecliptic longitude definition (the astrological definition) for far too long. There is no reason to change the definition (until we move to Mars... or maybe Saturn).
Frank Reed