NavList:
A Community Devoted to the Preservation and Practice of Celestial Navigation and Other Methods of Traditional Wayfinding
From: Andrés Ruiz
Date: 2009 Nov 5, 11:01 +0100
For this singular case
using Van Allen we obtain:
c1 = c2 =0
B = D = E = F = 0
And K, J, G, H are
See http://www.navlist.net?i=030630&y=200606 for implementation of Van Allen’s method
Of course variations on
the original method are possible in order to avid singularities.
Andrés Ruiz
Navigational Algorithms
http://sites.google.com/site/navigationalalgorithms/
De:
Enviado el: miércoles, 04 de
noviembre de 2009 20:36
Para:
Asunto: [NavList 10442] Re:
Two-body fix caveat
I don't have a copy of
Van Allen's paper, I only read it once months ago in a library, so my memory is
taking its time to reengage on this issue… :-) Now I have another
idea why Andres might have gotten "no answer" from Van Allen's method
for our test case.
The method consists of the following steps:
1) The LOPs define two planes in 3-D space,
2) The intersection of these two planes defines a straight line in 3-D,
3) The intersections of this straight line with the Earth's surface are the two
fixes,
4) Results of Step 3) are translated into latitude and longitude.
The straight line from Step 2) has to be parametrized somehow; and it is the
value of that parameter that is extracted in Step 3) from a quadratic
equation. There is some freedom in choosing this parameter, which
is accompanied by a problem that really cannot be solved within this method,
only addressed by an extra step.
I chose this parameter to be the Cartesian coordinate z, which is aligned with
the Earth's axis of rotation. This coordinate has therefore a one-to-one
correspondence with latitude. If the two celestial bodies are on the same
meridian, then the two fixes, while still distinct, have the same latitude,
which invalidates Step 3). That is because the straight line from Step 2)
is parallel to the equatorial plane (same latitude everywhere). Hence the
coordinate z is not a suitable parameter in this case. My spreadsheet
handles this issue by testing for the GHA1=GHA2 condition (within some
numerical tolerance) and solving the problem in an auxiliary coordinate system
rotated by 90 degrees with respect to convention. The solution is then
translated back to the original xyz and thus readied for Step 4).
I remember with 99% certainty that Van Allen chose the coordinate x to be this
straight-line parameter. With this choice his original method will fail
if the two bodies have the same declination, which is precisely the case with
my artificial test case. Andres, could this be causing the NaN's you saw?
(just trying to make a semi-educated guess here). Perhaps you can detune
the GPs a bit and see what happens. If I'm right then moving one GP N/S
will eliminate this problem, while moving it E/W will not help.
The Van Allen's method also does not like 90-degree separations in longitude,
which can lead to divisions by zero in some cases. My spreadsheet
therefore works with its own "Prime Meridian" selected halfway
between GHA1 and GHA2. Even then the method will fail when the two bodies
are separated by 180 degrees (i.e. sun and full moon) but that is a poor
arrangement to begin with and shouldn't be used in the first place.
Finally, a body exactly above a pole (how likely is that? :-) ) also causes a
problem; here I went for the easy solution of "detuning" its
declination ever so slightly from plus or minus 90 degrees…
To summarize, if I had been aware of John Karl's two-body solution (or better
versed in spherical trigonometry to find it myself), I would certainly have
used it in lops.xls. A similar observation goes for Andres's clever
vector solution. The few caveats we are discussing now are minor compared
to the laboriousness of the Van Allen's method. Sometimes (often, in
fact) the intuitively clearest approach is not the most practical.
Peter Hakel
From: P H
<pmh099@yahoo.com>
To:
Sent: Wed, November 4, 2009
9:21:22 AM
Subject: [NavList 10438] Re:
Two-body fix caveat
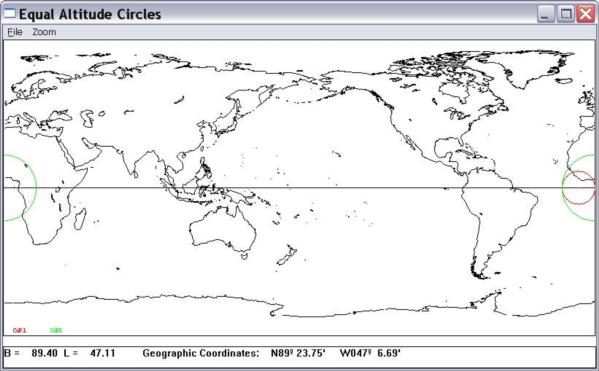
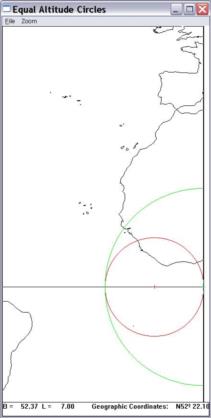
The Van Allen's method works fine for me even in this
singular case, see the attached screenshot of the lops.xls spreadsheet.
At the core of this method is a solution of a quadratic
equation whose discriminant D, as always, defines three cases:
D>0, two distinct solutions (LOPs intersect, the
usual CelNav case)
D=0, one solution (LOPs touch, like in this artificial
test case)
D<0, no solution
I was concerned about round-off errors for the D=0 case
when I was writing that spreadsheet. If D comes out ever so slightly
negative instead of zero, then SQRT(D) has a problem. So far, however,
Excel numerics has passed all such tests OK, including this one.
Peter Hakel
From:
To:
Sent: Wed, November 4, 2009
2:12:28 AM
Subject: [NavList 10426] Re:
Two-body fix caveat
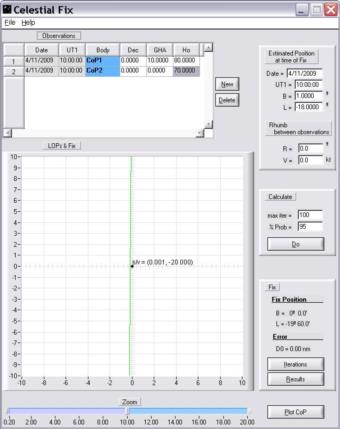
Solving this singular case with Van Allen’s
method: no solution. Vector Solution works fine.
An analytical solution of
the two star sight problem of celestial navigation
James A. Van Allen.
NAVIGATION Vol. 28, No. 1, 1981
iter Err
Be Le B1
L1 B2 L2 GHA1f dec1f
GHA2f dec2f
0
NaN NaN NaN NaN NaN
NaN
I1:
NaN
I2:
NaN
Vector Solution for the
Intersection of two Circles of Equal Altitude
THE JOURNAL OF NAVIGATION
(2008), 61, 355-365. The Royal Institute of Navigation
Andrés Ruiz González - Navigational Algorithms - http://sites.google.com/site/navigationalalgorithms/
iter Err
Be Le B1
L1 B2 L2 GHA1f dec1f
GHA2f dec2f
0 134.146176409012696
0.000058 -20.000000 0.000058
-20.000000 0.000001 -20.000000
10.000000 0.000010 0.000000 -0.000010
I1: 0.00000 -20.000000
I2: 0.00000 -20.000000
Andrés Ruiz
Navigational Algorithms
http://sites.google.com/site/navigationalalgorithms/
--~--~---------~--~----~------------~-------~--~----~
NavList message boards: www.navlist.net
Or post by email to: NavList@navlist.net
To , email NavList+@navlist.net
-~----------~----~----~----~------~----~------~--~---