NavList:

Steve Bryant, you wrote:
"Is there now and/or has there ever been a practical use (as a hobbyist or seagoer) for observing the moons of any planet as a means in the determination of one's position on earth; and, if so, how were/are those moons observable much less identifiable given typical optical means available to the sailor?"

Yes, absolutely this was practical. But only on land --completely impractical at sea.

The moons of Jupiter were used as an absolute time standard, rather like a natural, celestial chronometer, starting in the 17th century, not long after they were discovered by Galileo in 1610. Despite some valiant attempts, beginning with Galileo himself, this is impossible from a ship at sea unless one has some sort of gyro-stabilized telescope, which of course was out of the question until the 21st century. On land it was a popular method for determining absolute time even after lunars became practical. Tables and charts of the motions of the Galilean moons of Jupiter were included in the Nautical Almanac & Astronomical Ephemeris from the very beginning, starting in 1767, and they were published in other resources long before that.

The moons of Jupiter go through various mutual phenomena where they occasionally pass in front of each other or align with each other, and they are also eclipsed by Jupiter's shadow, which projects usually somewhat to one side of Jupiter as seen from Earth, and they and their shadows also transit the face of the giant planet. The closest of the great moons, Io, passes into Jupiter's shadow quite abruptly, and it is possible to determine the time of an eclipse to within one minute. Two observers in different places on Earth can observe the same eclipse of Io and record the local time when this occurs. The eclipse is simultaneous in the sense of absolute time. If those observers had phones (needless to say, rendering the observation pointless!), they could chat during the eclipse and they would see the same event at the same time. But one observer might see it at 3:15am local time while the other sees it at 6:35am local time. Those local times, by the way, could be accurate sundial times from the previous day carried forward by a common watch. That difference in time of 3 hours and 20 minutes is then converted to a difference in longitude at the usual rate of 15 degrees per hour (360/24 is 15), which would amount to 45 + 5 or 50 degrees difference in longitude for the case at hand. Assuming a +/- 1 minute accuracy in observation of the eclipse of the moon and a smaller, negligible uncertainty in the observation of the local time, this longitude difference would be accurate to about 0.25 degrees.

The moons of Jupiter can be used as a clock in this fashion, but that is all they are: an absolute time measure. They replace a chronometer in celestial navigation. Latitude and longitude can then be determined by any of the usual methods available, either historical or modern. It's all the same. Note, too, that this technique for determining longitude differences works whether we have an exact model of the motions of the moons, or not. But if we can accurately predict the absolute times of the eclipses, then we do not need to communicate with other observers for the determination of longitude. A pre-caculated ephemeris will immediately tell us our longitude difference from some arbitrary "prime" meridian. On the other hand, if we lack detailed predictions, we can still get longitude differences by writing to other observers and asking them to share the local times at which they observed the event in question. The method works for mapping purposes whether we have an ephemeris or not.

It is not difficult to identify the great moons of Jupiter. Any average observer with a small telescope can do it. There are four of them: Io, Europe, Ganymede, and Callisto, in order from nearest to farthest from Jupiter. Naturally they follow Kepler's Third Law so the orbital periods of the moons are proportional to the square root of the mean distances from Jupiter cubed. So even if we have no charts of their expected positions, they can be identified by their relative motions after a few hours of observation.

Incidentally, even this bit of basic navigational science has been occasionally abused. One fruitcake in particular, the crackpot historian Gavin Menzies, suggested that the Chinese in the 15th century used the moons of Jupiter to determine longitude. The guy's a real quack, and when he learned that some observers with excellent vision can visually detect the outermost moon(s) of Jupiter at their greatest distance from the planet, he jumped to the absurd conclusion that visual observers could detect the eclipses and other time-dependent events among the moons --ludicrous nonsense.

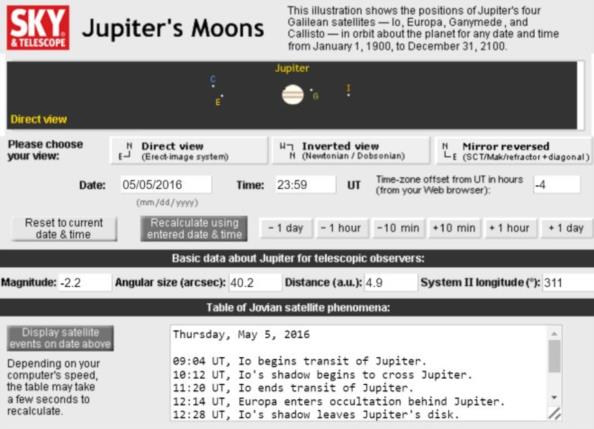
If you would like to experiment with observing the moons of Jupiter and get UT from their eclipses and other events, there's a nice little web app that's been available for something like a dozen years on the Sky & Telescope web site: jupiters-moons-javascript-utility. Attached below is a typical screen displaying the moons and their events for this evening. And if you read the directions and article down to the end, you'll discover that the single comment on the app is from someone in the UK who uses it in discussions of navigation and longitude. Note that this is very old-fashioned code, and it may be susceptible to problems and bugs, now and in the near future (including, for example, the use of javascript's "with" capability which Andrew Nikitin discussed in relation to another online app earlier this year). There are many other similar tools and apps that may be superior. I mention this one, in fact, because it is old and traditional in style.

Frank Reed

File: