NavList:

Dear Geoff,

Dear All,

As a complement to my last contribution, I am offering the following [almost] complete solution to the Observer's position when he took his awesome picture.

I submitted the results here-under to the Photographer and I will keep you posted about his own reply.

(1) - A few partial solutions have been published, to which I am offering the following comments :

(1.1) - The MonViso Azimuth seen from the Observer's position is close - but not identical - to the "departure course" determined through geodesic curves (e.g. the Vincenty method) because both differ by about to +/- 0.15°in this specific case. Hence, in a strict mathematical sense such geodesic curves are somewhat irrelevant to solve for an Azimuth of a distant body on an Ellipsoid.

(1.2) - Solving for an Azimuth of a distant body on an Ellipsoid just requires this distant body 3D coordinates in the Observer's local horizontal system. From the Observer's and distant target Coordinates (geographical Latitude, Longitude and Elevation above the Ellipsoid) you can quite easily get its distance - distances are invariant to the reference systems - but its azimuth is more delicate to determine. Nonetheless, I have extensively used such kind of computations. 

(2) - Further to much more in depth work, here are the following END RESULTS (check the enclosed attachment):

(2.1) - 2 D Plan studies

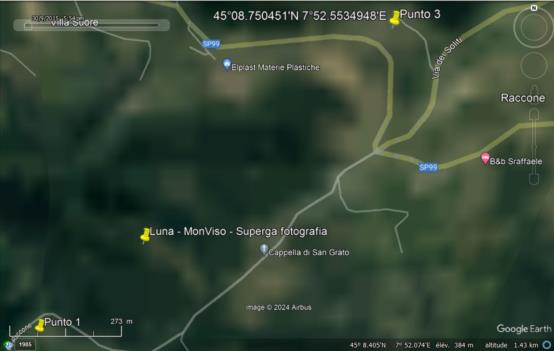
(2.1.1) - First, on a 2D plan, the Observer’s probable position is close to 10.600 meters from Basilica Superga in its Azimuth 049.5° at Position "Punto 2" (45°08.576'N 007°52.262'E, Google Earth Altitude at 427m , not showing on the attachment since it is so close from the final result).

(2.1.2) - On a 2D plan again, the extreme possible values for the Photographer's positions are between "Punto 1" (45°08.401N 007°51.970'E Google Earth Altitude at 360 m) and "Punto 3" (45°08.750'N 007°52.553').

(2.1.3) - The lateral error of the straight line between Punto 1 and Punto 3 should be quite small - most probably [much] less than 5 meters each side of this line - because the alignment between MonViso and Superga is deadly accurate.

(2.1.4) - From  the Software I am currently using, the picture was taken at a UT time close to 17h53m12s , or a local time in Torino very close to 18h53m12s +/- 15 seconds of time on Dec. 15th, 2023 as indicated.

(2.2) - 3D Studies

(2.2.1) - In the vicinity of the picture spot, the terrain goes uphill a lot. It gives additional constraints on the position since the elevation of the Superga steeple varies dramatically with its distance. And you have to respect realistic refraction values on both MonViso and Superga.

(2.2.3) -Best guess : The picture was taken at 17h53m12s UT (on Dec 15th, 2023)  with the Photographer at position 45°08.511'N 007°52.154'E and at an altitude of 381 m.

He was at a straight line distance of 10.452 km from the Superga steeple and of 80.776 km from MonViso.

From the Observer's position and at 17h53m12s UT (with TT-UT = +69.2s) Lady Moon refracted Upper Limb was at 2°17.743' , unrefracted Upper Limb at 2°01.777' and the refracted positions of MonViso at 2°16.7' and Superga Steeple at 2.06.6', with refraction to MonViso equal to 5.663' and to Superga Steeple equal to 1.183'. As always, extra digits to derive meaningful trends which are obtained through differences.

Best Regards,

Kermit

Last important notes :

(1) - These computations were carried out on WGS84 from Google Earth data. Google Earth altitudes assumed to be measured from WGS84 Ellipsoid. Is it actually the case ?

(2) - Any available exiting available theory to pre-compute refraction between 2 nearby points knowing Positions and Altitudes of departing and arrival points ?

Here the observed refraction at 5.6' to MonViso and 1.1' to Superga seem realistic, but do remain unconfirmed to date.

(3) - EXTRA-PUZZLE :

When can such scenario happen again ? It should be fairly simple to determine a good method for a quick search in Tables listing Moon Greenwich Hour Angle, Declination and Horizontal Parallax, e.g. the Nautical Almanac.

Any Taker here ?

File: