NavList:
A Community Devoted to the Preservation and Practice of Celestial Navigation and Other Methods of Traditional Wayfinding
From: Andrés Ruiz
Date: 2023 Dec 22, 10:07 -0800
Thanks Antoine for this interesting issue.
Solution for the example in "231217-LAN-Part-I-Near-Noon-methods-comparison-.pdf"
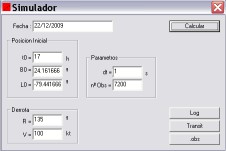
- EX1.Kermit.obs input file for Nautical Astronomy.exe (I did it quickly and I do not know if I interpret Hmoon data correctly)
- EX1.Kermit.current.png
- EX1.Kermit.png
231219-LAN-Part-II-Culmination-to-Meridan-Passage-fully-solved-.pdf
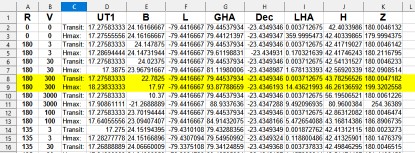
- LoogBook.xlsx (in zip file) simulated data, B1 example, for anyone who wants to play with it.
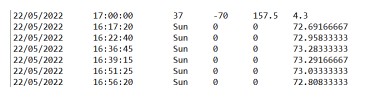
t | B2 | L2 | gha | dec | Hc | Zn | Event | |||||
5.9058333 | 60.115377 | -143.136 | 143.13203 | 1.5349944 | 31.419617 | 179.99534 |
| 05:54:21 | Meridian transit | 60º 6.9' | 143º 8.2' | |
5.9061111 | 60.115171 | -143.1358 | 143.13607 | 1.5350719 | 31.419901 | 180.00031 |
| 05:54:22 | Meridian transit | 60º 6.9' | 143º 8.1' | |
6.3288889 | 59.801256 | -142.8163 | 149.27507 | 1.6530247 | 31.636764 | 187.58909 |
| 06:19:44 | Culmination | 59º 48.1' | 142º 49.0' |
It is also interesting to compare with the SR solution as described on paper Celestial Fix - n LoPs - by Least squares Sight Reduction algorithm. Paper & Excel (B1solution.MP.png, B1solution.SR)
Back in 2009 I made a lot of simulation, huge amount of data, to see how time of culmination differs from time of meridian passage: simulacion V.xls, RV 135 100.7z
And conclude that Jim Wilson's method gives bad results when SOG is greater than say 10 kn.
Background
At culmination celestial body altitude H = maximum/minimum -> dH/dt = 0
Meridian passage:
- LHA = 0 (Upper Meridian of Place) or LHA = 180º (Lower Meridian of a Place)
- Azimuth Zn = 180º/0º
References (attached files):
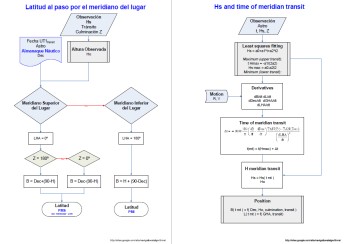
Pages from A1 - Algoritmos.pdf
- Latitude by meridian transit (Latitud al paso por el meridiano del lugar)
- Position by meridian transit (Hs and time of meridian transit)
- Ex-meridian sight (Latitud por altura circunmeridiana)
Pages from Position&Time.pdf
- The equations of the observations: Altitude
- Time derivatives
- Stationary observer
To solve this problem, I use a matrix integration of all differential equations for each observation, (see Position&Time.pdf).
Fair winds and following seas!
--
Andrés Ruiz
Navigational Algorithms
https://sites.google.com/site/navigationalalgorithms/