NavList:

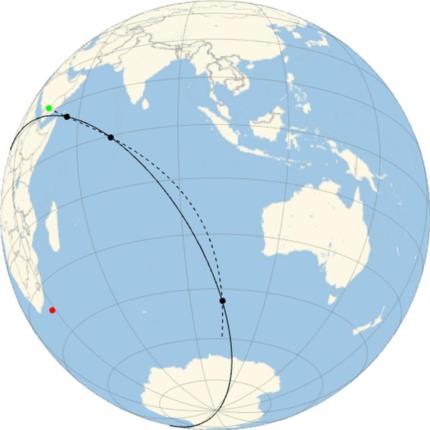
In my previous post I constructed a counter example to prove that an isoazimuth is not a small circle. In the example constructed the isoazimuth intersects the small circle at 3 points. Hence it follows that if you cross an LoP of equal altitude taken on one body with an LoP taken on another, there could be 3 valid solutions. This is consistent with the isoazimuths satisfying 3rd order equations. In order to get a better handle on what was happening I have plotted the izoazimuth and the small circle through the points P1, P2 and P4 given previously. (Note I had forgotten to state that the isoazimuth corresponds to an azimuth of 306° to the GP). The attached image shows what is going on. The GP is indicated by the green dot and the red dot is the pole of the circle passing through the points P1, P2 and P4 plotted in black. The izoazimuth is shown as the dashed curve. The izoazimuth will end at the pole. This intuitively clear since there will be some point near the pole where the azimuth of the GP is 306°. In fact very close to the pole you could travel a short distance and make the azimuth anything you like!

The points and curves in the image were all computed using the properties of circles on the complex plane discussed here and the properties of the Littrow projection.

Robin Stuart

File: