NavList:
A Community Devoted to the Preservation and Practice of Celestial Navigation and Other Methods of Traditional Wayfinding
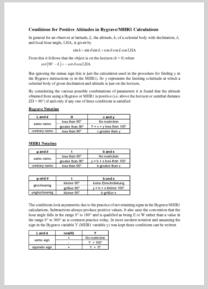
Comments on Bygrave/MHR1 calculations
From: Robin Stuart
Date: 2016 Aug 4, 12:55 -0700
From: Robin Stuart
Date: 2016 Aug 4, 12:55 -0700
Having now played around a bit with a working model MHR1 I have a few comments and observations
Instructions for using Bygrave and MHR1 slide rules referred to here have been posted by Gary Lapook
https://NavList.net/m2.aspx/Bygrave-slide-rule-LaPook-sep-2008-g6329
https://NavList.net/m2.aspx/Uboat-Celestial-Navigation-WWII-LaPook-jan-2016-g34163
- When compared they are identical except for the method used to compute azimuth A. Whereas the MHR1 emphasizes in bold letters and an exclamation point “Az stets kleiner 90° ablesen!” (Always read off Az less than 90°!). There is no such rule for the Bygrave. Does this reflect a difference in conventions and practice between Britain and Germany at the time or does the emphasis represent a departure from standard practice? Overall it seems to me that the Bygrave method is a bit more straightforward in practice. The Bygrave instructions however are surprisingly lacking in explicit details of how exactly to compute the azimuth and the user is left to deduce it from the figure. It would have been helpful if the Bygrave instructions included a clear statement like “Azimuth is measured from the lower pole east or west in accordance with the hour angle, H”.
- The Bygrave and MHR1 are able to do very little more than the task they were designed for i.e. perform sight reduction. In that case one can safely assume that the celestial body being observed is visible and therefore above the horizon. The instructions as given do not allow the user to determine whether the altitude is positive or negative (Zenithal Distance less than or greater than 90°) for an arbitrary input set of latitude, declination and hour angle values. This also means that when the Bygrave is used to compute Great Circle courses there is an ambiguity as to whether the course is greater or less than 90° (5400nm) in length. Maybe for this reason the example in the Bygrave instructions considers a distance of 4127nm. It turns out however that intermediate values computed in the course of the sight reduction can be used to quite easily determine whether an altitude is positive or negative by checking just three conditions. This extends the usefulness of these slide rules somewhat. I have described it in the attachment.
- Certain calculations that look like they should be doable using a Bygrave or MHR1 do not seem to be possible. For example the LHA and hence time at which a particular body rises or sets is given by cos( 90° - LHA ) = tan δ tan L . I cannot see how it can be done on cylindrical slide rules but would be interesting in suggestions.
Robin Stuart